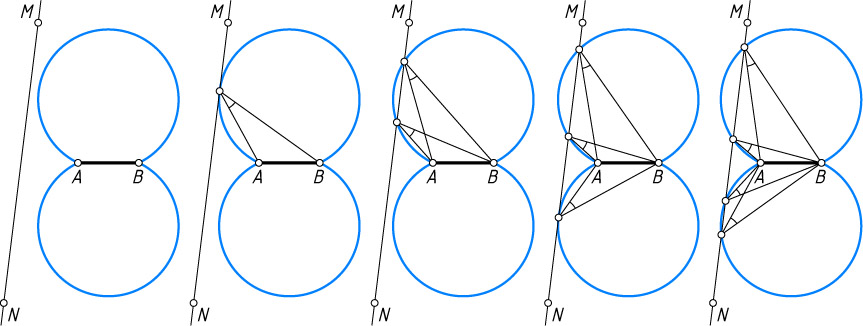
277. С помощью циркуля и линейки на данной прямой MN
постройте точку, из которой данный отрезок AB
был бы виден под данным углом.
Указание. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (см. задачи 12 и 2889).
Решение. Построим геометрическое место точек, из которых данный отрезок AB
был бы виден под данным углом (см. задачу 2889) — фигуру, состоящую из двух дуг равных окружностей. Искомые точки — это точки пересечения прямой MN
с этой фигурой.
Количество решений совпадает с количеством общих точек построенной фигуры и данной прямой (0, 1, 2, 3, 4).
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 58, с. 39
