279. Задача Потено. На плоскости даны два отрезка a
и b
. С помощью циркуля и линейки постройте точку, из которой отрезок a
был бы виден под данным углом \alpha
, а отрезок b
— под данным углом \beta
.
Указание. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (см. задачи 12 и 2889).
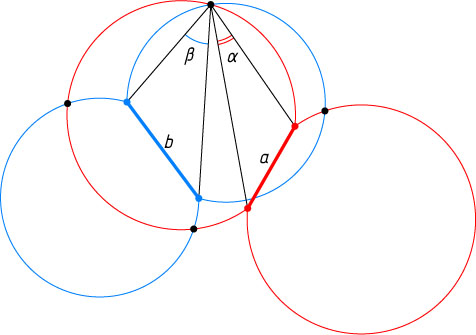
Решение. Построим геометрическое место точек, из которых отрезок a
виден под углом \alpha
— две дуги равных окружностей (см. задачи 2889 и 12), и геометрическое место точек, из которых отрезок b
виден под углом \beta
— две дуги равных окружностей.
Пересечение двух построенных геометрических мест (если оно есть) даёт искомые точки.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 61, с. 40
