312. Стороны треугольника равны 10, 10, 12. Найдите радиусы вписанной и вневписанных окружностей.
Ответ. 3; 12; 8; 8.
Указание. Радиус вневписанной окружности, касающейся основания, можно найти из подобия треугольников. Радиус вневписанной окружности, касающейся боковой стороны, равен высоте, опущенной на основание.
Решение. Пусть r
— радиус вписанной окружности треугольника ABC
(AC=BC=10
, AB=12
), r_{c}
, r_{b}
и r_{a}
— радиусы вневписанных окружностей, касающихся сторон AB
, AC
и BC
соответственно, O_{c}
, O_{b}
и O_{a}
— их центры, S
— площадь треугольника ABC
, p
— его полупериметр.
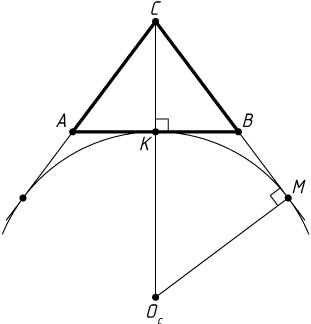
Первый способ. Поскольку высота CK
треугольника ABC
равна 8, то S=48
(рис. 1). Следовательно,
r=\frac{S}{p}=\frac{48}{16}=3.
Если окружность с центром O_{c}
касается продолжения стороны BC
в точке M
, то из подобия треугольников CMO_{c}
и CKB
находим, что
r_{c}=O_{c}M=BK\cdot\frac{CM}{CK}=BK\cdot\frac{BC+BM}{CK}=
=BK\cdot\frac{BC+BK}{CK}=6\cdot\frac{16}{8}=12.
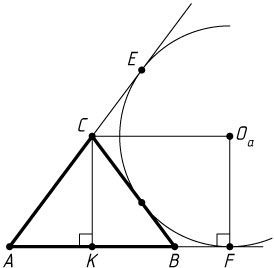
Пусть окружность с центром O_{a}
касается продолжения стороны AB
в точке F
, а продолжения стороны AC
— в точке E
(рис. 2). Поскольку CO_{a}
— биссектриса угла BCE
, а CK
— биссектриса его смежного угла ACB
, то \angle O_{a}CK=90^{\circ}
. Поэтому O_{a}CKF
— прямоугольник. Следовательно,
r_{b}=r_{a}=O_{a}F=CK=8.
Второй способ. Пусть a
, b
и c
— стороны произвольного треугольника, S
— его площадь, p
— полупериметр, r
— радиус вписанной окружности, r_{a}
, r_{b}
и r_{c}
— радиусы вневписанных окружностей, касающихся сторон a
, b
и c
соответственно. Тогда
r=\frac{S}{p},~r_{a}=\frac{S}{p-a}
(см. задачи 452 и 392). В нашем случае
r=\frac{S}{p}=\frac{48}{16}=32,~r_{c}=\frac{S}{p-c}=\frac{48}{16-12}=12,
r_{b}=r_{a}=\frac{S}{p-a}=\frac{48}{16-10}=8.
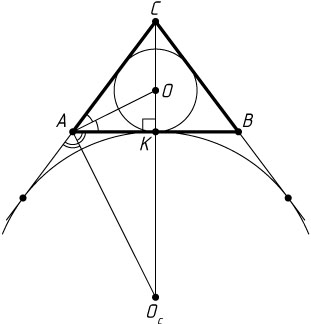
Третий способ. Оставим обозначения, принятые в предыдущих способах. Поскольку AO
— биссектриса треугольника AKC
(рис. 3), то
\frac{OK}{OC}=\frac{AK}{AC}=\frac{6}{10}=\frac{3}{5},
а так как OK=r
, то
r=OK=\frac{3}{8}CK=\frac{3}{8}\cdot8=3.
Поскольку AO_{c}
— биссектриса внешнего угла треугольника AKC
, то
\frac{O_{c}K}{O_{c}C}=\frac{AK}{AC}=\frac{6}{10}=\frac{3}{5},
а так как O_{c}K=r_{c}
, то
r_{c}=O_{c}K=\frac{3}{2}CK=\frac{3}{2}\cdot8=12.
Поскольку CO_{a}
— биссектриса угла BCE
, а CK
— биссектриса его смежного угла ACB
, то \angle O_{a}CK=90^{\circ}
. Поэтому O_{a}CKF
— прямоугольник. Следовательно,
r_{b}=r_{a}=O_{a}F=CK=8.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 229, с. 23
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 82


