331. Около окружности описана трапеция ABCD
, боковая сторона AB
перпендикулярна основаниям, M
— точка пересечения диагоналей трапеции. Площадь треугольника CMD
равна S
. Найдите радиус окружности.
Ответ. \sqrt{S}
.
Указание. Докажите, что треугольники BAM
и DMC
равновелики (см. задачу 3017), а расстояние от точки M
до стороны AB
равно радиусу окружности.
Решение. Поскольку треугольники BAC
и BDC
равновелики, а треугольник BMC
— их общая часть, то площадь треугольника AMB
также равна S
.
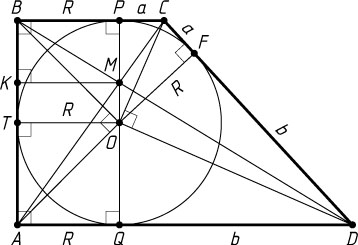
Пусть O
— центр окружности; R
— её радиус; P
, F
и Q
— точки касания со сторонами BC
, CD
и AD
соответственно; K
— проекция точки M
на сторону AB
. Тогда
CF=CP=BC-BP=BC-R,~DF=DQ=AD-AQ=AD-R.
В прямоугольном треугольнике COD
(см. задачу 313) известно, что
R^{2}=OF^{2}=CF\cdot DF=(BC-R)(AD-R).
Отсюда находим, что R=\frac{AD\cdot BC}{AD+BC}
.
С другой стороны, из подобия треугольников AKM
и ABC
следует, что KM=\frac{BC\cdot AM}{AC}
, а из подобия треугольников AMD
и CMB
—
\frac{AM}{AC}=\frac{AD}{AD+BC}.
Поэтому KM=\frac{BC\cdot AD}{AD+BC}=R
.
Поскольку AB=2R
, то
S=S_{\triangle AMB}=\frac{1}{2}AB\cdot KM=\frac{1}{2}2R\cdot R=R^{2}.
Следовательно, R=\sqrt{S}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 263, с. 213
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.38, с. 33
