353. Периметр треугольника ABC
равен 8. В треугольник вписана окружность и к ней проведена касательная, параллельная стороне AB
. Отрезок этой касательной, заключённый между сторонами AC
и CB
, равен 1. Найдите сторону AB
.
Ответ. 2.
Указание. Отсечённый треугольник подобен данному с коэффициентом, равным отношению их периметров.
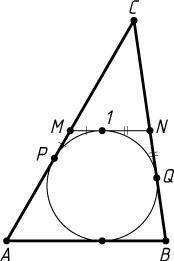
Решение. Обозначим точки пересечения касательной со сторонами AC
и CB
через M
и N
, а точки касания этих сторон с вписанной окружностью — через P
и Q
. Тогда полупериметр треугольника CMN
равен CP=CQ=4-AB
(см. задачи 4805 и 219). Из подобия треугольников CMN
и CAB
следует, что
\frac{MN}{AB}=\frac{4-AB}{4},~\mbox{или}~\frac{1}{AB}=\frac{4-AB}{4}.
Из этого уравнения находим, что AB=2
.
Источник: Вступительный экзамен в МИРЭА. —
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.34, с. 88
