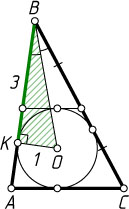
355. Окружность радиуса 1 вписана в треугольник ABC
, в котором \cos\angle B=0{,}8
. Эта окружность касается средней линии треугольника ABC
, параллельной стороне AC
. Найдите сторону AC
.
Ответ. 3.
Указание. Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности полупериметра и противолежащей стороны (см. задачу 219).
Решение. Пусть O
— центр вписанной окружности, K
— её точка касания со стороной AB
. Тогда
\tg\frac{1}{2}\angle B=\frac{\sin\angle B}{1+\cos\angle B}=\frac{0{,}6}{1+0{,}8}=\frac{1}{3}.
Поэтому
BK=\frac{OK}{\tg\frac{1}{2}\angle B}=3.
С другой стороны, отрезок BK
равен полупериметру отсечённого треугольника (см. задачу 4805), который подобен данному с коэффициентом \frac{1}{2}
. Поэтому полупериметр данного треугольника равен 6. Следовательно, AC=6-BK=3
(см. задачу 219).
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1974, № 3, вариант 3, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 278
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 252, с. 14
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 170, с. 20
