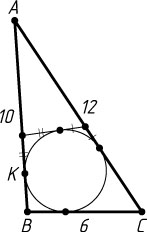
377. В треугольник со сторонами 6, 10, и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника.
Ответ. 16.
Указание. Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности полупериметра и противолежащей стороны.
Решение. Пусть K
— точка касания окружности, вписанной в треугольник ABC
, со стороной AB
(AB=10
, AC=12
, BC=6
).
Если p
— полупериметр треугольника, то
AK=p-BC=14-6=8
(см. задачу 219), а длина отрезка AK
равна полупериметру отсечённого треугольника (см. задачу 4805).
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.373, с. 183
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.27, с. 88
