380. Три окружности радиусов 1, 2 и 3 касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей.
Ответ. 1.
Указание. Докажите, что искомая окружность совпадает с окружностью, вписанной в треугольник с вершинами в центрах трёх данных окружностей.
Решение. Пусть C
, B
и A
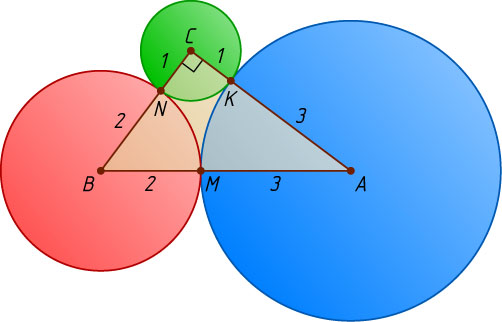
— центры окружностей радиусов 1, 2 и 3 соответственно (рис. 1). Линия центров двух касающихся окружностей проходит через точку их касания, значит, точки M
, N
и K
касания окружностей лежат на сторонах треугольника ABC
. Пусть точка K
лежит на отрезке AC
, точка M
— на отрезке AB
, точка N
— на отрезке BC
. Тогда
AB=AM+MB=3+2=5,~AC=AK+KC=3+1=4,~BC=BN+NC=2+1=3.
Треугольник ABC
— прямоугольный, так как AC^{2}+BC^{2}=16+9=25=AB^{2}
, значит, радиус его вписанной окружности равен \frac{AC+BC-AB}{2}=\frac{3+4-5}{2}=1
(см. задачу 217).
Докажем, что окружность, проходящая через точки K
, M
, N
, и есть вписанная окружность треугольника ABC
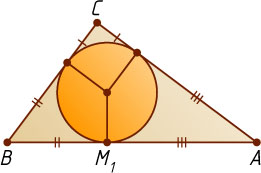
. Действительно, если вписанная окружность треугольника ABC
касается стороны AB
в точке M_{1}
(рис. 2), то AM_{1}=\frac{AB+AC-BC}{2}=\frac{5+4-3}{2}=3=AM
(см. задачу 219), значит, точка M_{1}
совпадает с точкой M
. Аналогично докажем, что вписанная окружность треугольника ABC
касается его сторон AC
и BC
соответственно в точках K
и N
.
Таким образом, радиус окружности, проходящей через точки касания данных окружностей, равен 1.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 164, с. 21
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 164, с. 19
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.32, с. 70

