381. В равносторонний треугольник со стороной a
вписана окружность. К окружности проведена касательная так, что её отрезок внутри треугольника равен b
. Найдите площадь треугольника, отсечённого этой касательной.
Ответ. \frac{a\sqrt{3}(a-2b)}{12}
.
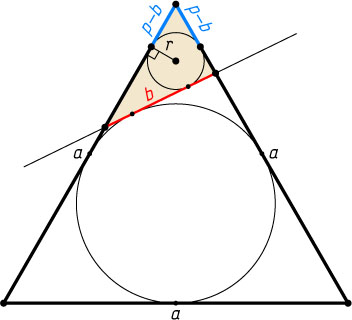
Указание. Впишите окружность в отсечённый треугольник.
Решение. Полупериметр p
отсечённого треугольника равен \frac{a}{2}
(см. задачу 4805). Впишем окружность в отсечённый треугольник. Расстояние от вершины угла, противоположного стороне, равной b
, до ближайшей точки касания с этой окружностью равно
p-b=\frac{a}{2}-b=\frac{a-2b}{2}
(см. задачу 219). Если r
— радиус этой окружности, а S
— искомая площадь, то
r=\frac{a-2b}{2\sqrt{3}},~S=pr=\frac{a\sqrt{3}(a-2b)}{12}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.405, с. 185
