458. В остроугольном треугольнике ABC
проведены высоты AM
и CN
, O
— центр описанной около ABC
окружности. Известно, что \angle ABC=\beta
, а площадь четырёхугольника NOMB
равна S
. Найдите AC
.
Ответ. 2\sqrt{S\tg\beta}
.
Указание. Диагонали четырёхугольника NOMB
взаимно перпендикулярны (см. задачу 480).
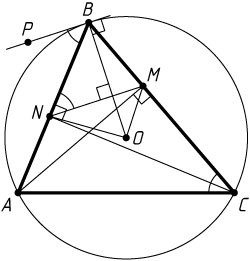
Решение. На касательной к описанной окружности данного треугольника отметим точку P
так, чтобы она и точка C
лежали по разные стороны от прямой AB
. Из теоремы об угле между касательной и хордой следует, что
\angle ABP=\angle ACB=\angle BNM,
поэтому BP\parallel MN
, а так как OB\perp BP
, то OB\perp MN
. Треугольник BMN
подобен треугольнику BAC
с коэффициентом \cos\beta
(см. задачу 19), значит, MN=AC\cos\beta
.
Пусть OB=R
— радиус описанной окружности треугольника ABC
. Тогда OB=R=\frac{AC}{2\sin\beta}
. Следовательно,
S=\frac{1}{2}MN\cdot OB=\frac{1}{2}AC\cos\beta\cdot\frac{AC}{2\sin\beta}=\frac{1}{4}AC^{2}\ctg\beta.
Отсюда находим, что AC=2\sqrt{S\tg\beta}
.
Источник: Вступительный экзамен на физический факультет МГУ. — 1985, вариант 1, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 42
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 212, с. 208
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 120
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 66, с. 144
