480. Теорема Нагеля. В треугольнике ABC
проведены высоты BB_{1}
и AA_{1}
; O
— центр описанной около треугольника ABC
окружности. Докажите, что прямые A_{1}B_{1}
и CO
перпендикулярны.
Указание. Выразите через угол BAC
сумму углов OCB
и CA_{1}B_{1}
.
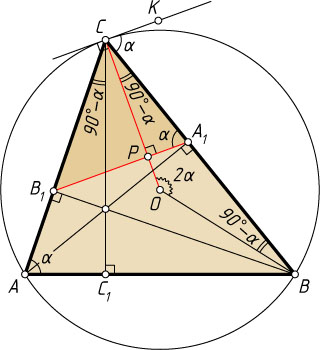
Решение. Первый способ. Пусть треугольник ABC
— остроугольный и \angle CAB=\alpha
. Тогда (см. задачу 19)
\angle CA_{1}B_{1}=\alpha,~\angle COB=2\alpha,~\angle OCB=90^{\circ}-\alpha.
Поэтому
\angle OCB+\angle B_{1}A_{1}C=\alpha+90^{\circ}-\alpha=90^{\circ}.
Для тупоугольного треугольника доказательство аналогично.
Второй способ. Треугольник A_{1}CB_{1}
подобен треугольнику ACB
(см. задачу 19). Пусть CC_{1}
— высота треугольника ACB
. Поскольку \angle OCB=\angle ACC_{1}
, высота CP
треугольника A_{1}CB_{1}
лежит на прямой CO
(см. задачу 20).
Третий способ. Проведём касательную CK
к описанной окружности треугольника ABC
(точки K
и A
лежат по разные стороны от прямой BC
). Из теоремы об угле между касательной и хордой следует, что
\angle BCK=\angle BAC=\angle CA_{1}B_{1}
(см. задачу 19). Значит, CK\parallel A_{1}B_{1}
, а так как OC\perp CK
, то OC\perp A_{1}B_{1}
.
Четвёртый способ. Пусть H
— ортоцентр треугольника ABC
. Из задачи 20 следует, что CH
и CO
— изогонали угла ACB
, а так как A_{1}
и B_{1}
— проекции точки H
на стороны угла, то CO\perp A_{1}B_{1}
(см. задачу 10618).
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 20
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 39, с. 185
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 9, с. 193
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 34, с. 60; № 14, с. 97
