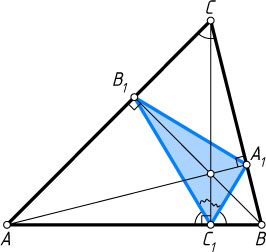
533. Докажите, что высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (т. е. треугольника с вершинами в основаниях высот данного).
Указание. Докажите, что если AA_{1}
и BB_{1}
— высоты треугольника ABC
, то \angle A_{1}C_{1}B=\angle ACB
(или воспользуйтесь утверждением задачи 1296).
Решение. Первый способ. Пусть A_{1}
, B_{1}
и C_{1}
— основания высот остроугольного треугольника ABC
, проведённых из вершин A
, B
и C
соответственно. Тогда (см. задачу 19)
\angle AC_{1}B_{1}=\angle ACB,~\angle BC_{1}A_{1}=\angle ACB.
Поэтому \angle AC_{1}B_{1}=\angle BC_{1}A_{1}
. Следовательно,
\angle B_{1}C_{1}C=90^{\circ}-\angle AC_{1}B_{1}=90^{\circ}-\angle BC_{1}A_{1}=\angle A_{1}C_{1}C.
Аналогично
\angle A_{1}B_{1}B=\angle C_{1}B_{1}B,~\angle B_{1}A_{1}A=\angle C_{1}A_{1}A.
Второй способ. Из утверждения задачи 1296 (теорема Бланше) следует, что лучи A_{1}A
, B_{1}B
и C_{1}C
— биссектрисы углов треугольника A_{1}B_{1}C_{1}
.
Примечание. 1. Если углы остроугольного треугольника равны \alpha
, \beta
и \gamma
, то соответствующие углы его ортотреугольника равны 180^{\circ}-2\alpha
, 180^{\circ}-2\beta
и 180^{\circ}-2\gamma
.
Например (см. задачу 141),
\angle B_{1}A_{1}C_{1}=180^{\circ}-\angle BA_{1}C_{1}-\angle CA_{1}B_{1}=180^{\circ}-\alpha-\alpha=180^{\circ}-\alpha.
Остальное аналогично.
2. Если треугольник тупоугольный, то две его высоты — биссектрисы внешних углов ортотреугольника, а третья — биссектриса внутреннего угла.
3. См. также статью А.Егорова «Ортоцентрический треугольник», Квант, 2001, N4, с.36-38.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 20
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 71, с. 82
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 75, с. 10
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 12, с. 183
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 4, с. 96
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.57(а), с. 17
