708. Окружность, вписанная в треугольник ABC
, касается стороны BC
в точке M
. Докажите, что окружности, вписанные в треугольники ABM
и ACM
, касаются отрезка AM
в одной точке.
Указание. См. задачу 219.
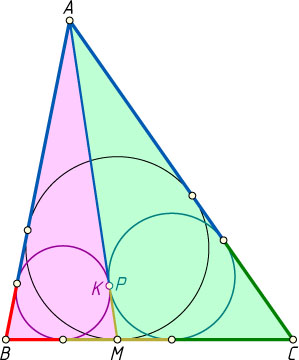
Решение. Пусть K
и P
— точки касания окружностей, вписанных в треугольники ABM
и ACM
, со стороной AM
; p_{1}
, p_{2}
, p
— полупериметры треугольников ABM
, ACM
и ABC
соответственно. Тогда
MK=p_{1}-AB,~MP=p_{2}-AC,~BM=p-AC,~CM=p-AB
(см. задачу 219), поэтому
MK-MP=p_{1}-AB-p_{2}+AC=p_{1}-p_{2}+AC-AB=
=\frac{AB-AC}{2}+\frac{BM-MC}{2}+AC-AB=\frac{BM-MC}{2}-\frac{AB-AC}{2}=
=\frac{p-AC-p+AB}{2}-\frac{AB-AC}{2}=\frac{AB-AC}{2}-\frac{AB-AC}{2}=0.
Следовательно, точки K
и P
совпадают.
Примечание. Это частный случай утверждения задачи 5418.
