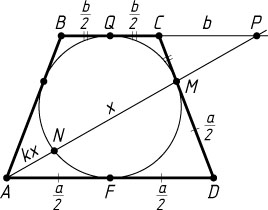
762. Равнобедренная трапеция с основаниями AD
и BC
(AD\gt BC
) описана около окружности, которая касается стороны CD
в точке M
. Отрезок AM
пересекает окружность в точке N
. Найдите отношение AD
к BC
, если AN:NM=k
.
Ответ. 8k-1
.
Указание. Примените теорему о касательной и секущей.
Решение. Первый способ. Обозначим AD=a
, BC=b
, MN=x
. Пусть Q
и F
— точки касания окружности со сторонами BC
и AB
соответственно. Тогда по теореме о касательной и секущей
AF^{2}=AM\cdot AN,~\mbox{или}~\frac{a^{2}}{4}=k(k+1)x^{2}.
Продолжим AM
до пересечения с прямой BC
в точке P
. Из подобия треугольников CPM
и DAM
следует, что \frac{CP}{CM}=\frac{AD}{DM}=2
. Поэтому CP=2CM=2CQ=b
.
По теореме о касательной и секущей
PQ^{2}=PN\cdot PM,~\mbox{или}~\frac{9b^{2}}{4}=\left(\frac{bx(k+1)}{a}+x\right)\cdot\frac{bx(k+1)}{a}
(так как PM=\frac{b}{a}\cdot AM
). Разделив почленно это равенство на доказанное ранее, получим, что 9bk=b(k+1)+a
. Отсюда находим, что \frac{a}{b}=8k-1
.
Второй способ. Обозначим AD=a
, BC=b
, MN=x
. Пусть Q
, F
и L
— точки касания окружности со сторонами BC
, AD
и AB
соответственно. Тогда ML=\frac{2ab}{a+b}
(см. задачу 1512), AF=\frac{a}{2}
.
Прямая LN
проходит через середину K
отрезка AF
(см. задачу 121). Из подобия треугольников ANK
и MNL
следует, что \frac{AK}{ML}=\frac{AN}{MN}
, или
\frac{\frac{a}{4}}{\frac{2ab}{a+b}}=k~\Leftrightarrow~\frac{a+b}{8b}=k~\Leftrightarrow~\frac{a}{b}+1=8k~\Leftrightarrow~\frac{a}{b}=8k-1.
Третий способ. Обозначим AD=a
, BC=b
, AN=n
, NM=m
, \angle ADC=\alpha
. Пусть CH
— высота трапеции, T
— точка касания вписанной окружности с основанием AD
. Тогда по теореме о касательной и секущей
\frac{a^{2}}{4}=AT^{2}=AN\cdot AM=n(n+m).
Трапеция ABCD
равнобедренная и описанная, поэтому
DH=\frac{AD-BC}{2}=\frac{a-b}{2},~CD=\frac{AD+BC}{2}=\frac{a+b}{2},
значит,
\cos\alpha=\cos\angle CDH=\frac{DH}{CD}=\frac{\frac{a-b}{2}}{\frac{a+b}{2}}=\frac{a-b}{a+b}.
По теореме косинусов
(n+m)^{2}=AM^{2}=AD^{2}+DM^{2}-2AD\cdot DM\cos\alpha=AD^{2}+DT^{2}-2AD\cdot DT\cos\alpha=
=a^{2}+\frac{a^{2}}{4}-2a\cdot\frac{a}{2}\cdot\frac{a-b}{a+b}=\frac{a^{2}}{4}\cdot\frac{a+9b}{a+b}.
Тогда
\frac{AT^{2}}{AM^{2}}=\frac{n(n+m)}{(n+m)^{2}}=\frac{\frac{a^{2}}{4}}{\frac{a^{2}}{4}\cdot\frac{a+9b}{a+b}},~\mbox{или}~\frac{n}{n+m}=\frac{a+b}{a+9b},~\frac{\frac{n}{m}}{\frac{n}{m}+1}=\frac{\frac{a}{b}+1}{\frac{a}{b}+9},
откуда
\frac{a}{b}=8\cdot\frac{n}{m}-1=8k-1.
Источник: Вступительный экзамен в МФТИ. — 1974, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 74-1-3, с. 168
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.33, с. 96
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 519, с. 132
