10051. Через точку P
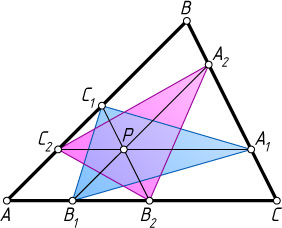
проведены три отрезка, параллельные сторонам треугольника ABC
(см. рисунок). Докажите, что площади треугольников A_{1}B_{1}C_{1}
и A_{2}B_{2}C_{2}
равны.
Решение. Заметим, что
S_{\triangle A_{2}B_{2}C_{2}}=S_{\triangle A_{2}C_{2}P}+S_{\triangle B_{2}C_{2}P}+S_{\triangle A_{2}B_{2}P},
S_{\triangle A_{1}B_{1}C_{1}}=S_{\triangle A_{1}C_{1}P}+S_{\triangle B_{1}C_{1}P}+S_{\triangle A_{1}B_{1}P}.
Докажем, что S_{\triangle A_{2}C_{2}P}=S_{\triangle A_{1}C_{1}P}
(для других пар площадей равенство доказывается аналогично). Это можно доказать различными способами.
Первый способ. Поскольку C_{2}PA_{2}B
— трапеция, то S_{\triangle C_{2}A_{2}P}=S_{\triangle BA_{2}P}
, а так как BC_{1}PA_{2}
— параллелограмм, то S_{\triangle BA_{2}P}=S_{\triangle BC_{1}P}
, наконец, из того, что BC_{1}PA_{1}
— трапеция, получим, что S_{\triangle BC_{1}P}=S_{\triangle A_{1}C_{1}P}
. Следовательно, S_{\triangle A_{2}C_{2}P}=S_{\triangle A_{1}C_{1}P}
. Что и требовалось доказать.
Второй способ. Пусть X
и Y
— основания перпендикуляров, опущенных из точек A_{2}
и C_{1}
на отрезок A_{1}C_{2}
. Тогда
S_{\triangle C_{2}A_{2}P}=C_{2}P\cdot A_{2}X~\mbox{и}~S_{\triangle C_{1}A_{1}P}=PA_{1}\cdot C_{1}Y.
Треугольники C_{2}C_{1}P
и PA_{2}A_{1}
подобны (соответствующие стороны параллельны), поэтому C_{1}Y:A_{2}X=C_{2}P:PA_{1}
, следовательно, S_{\triangle A_{2}C_{2}P}=S_{\triangle A_{1}C_{1}P}
.
Третий способ. Докажем, что
S_{\triangle B_{2}AC_{2}}+S_{\triangle C_{2}BA_{2}}+S_{\triangle A_{2}CB_{2}}=S_{\triangle B_{1}AC_{1}}+S_{\triangle C_{1}BA_{1}}+S_{\triangle A_{1}CB_{1}}.
Не теряя общности, можно считать, что площадь треугольника ABC
равна 1.
Пусть
AB_{2}:B_{2}C=p:(1-p),~CA_{2}:A_{2}B=q:(1-q),~BC_{2}:C_{2}A=r:(1-r).
Тогда, используя отношение площадей треугольников с общим углом (см. задачу 3007), получим, что
S_{\triangle B_{2}AC_{2}}=p(1-r),~S_{\triangle C_{2}BA_{2}}=r(1-q),~S_{\triangle A_{2}CB_{2}}=q(1-p),
т. е.
S_{\triangle B_{2}AC_{2}}+S_{\triangle C_{2}BA_{2}}+S_{\triangle A_{2}CB_{2}}=p+q+r-pr-pq-rq.
Из теоремы о пропорциональных отрезках (см. задачу 1059) следует, что
AB_{1}:AC=1-q,~AC_{1}:AB=p,~BA_{1}:BC=r.
Следовательно,
S_{\triangle B_{1}AC_{1}}+S_{\triangle C_{1}BA_{1}}+S_{\triangle A_{1}CB_{1}}=
=(1-q)p+r(1-p)+q(1-r)=p+q+r-pr-pq-rq.
Что и требовалось доказать.
Источник: Всероссийская олимпиада школьников. — 2015-2016, XLII, окружной этап, 10 класс
