10315. Правильный треугольник ABC
вписан в окружность. Прямая, проходящая через середину стороны AB
и параллельная AC
, пересекает дугу AB
, не содержащую C
, в точке K
. Докажите, что отношение \frac{AK}{BK}
равно отношению стороны правильного пятиугольника к его диагонали.
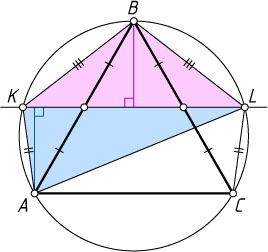
Решение. Пусть L
— вторая точка пересечения прямой с окружностью Тогда дуги CL
и AK
, заключённые между параллельными хордами AC
и KL
, равны. Значит, равны хорды CL
и AK
. Кроме того, треугольник ABC
правильный, поэтому равны дуги CLB
и AKB
, значит, хорды BL
и BK
стягивают равные дуги. Следовательно, BL=BK
. Тогда (см. задачу 17)
AL=BL+CL=BK+AK.
С другой стороны, прямая KL
делит сторону AB
пополам, поэтому высоты треугольников AKL
и BKL
, опущенные на общую сторону KL
, равны, а значит, равны их площади. Следовательно,
AK\cdot AL=BK\cdot BL=BK^{2},
откуда
\frac{AK}{BK}\cdot\frac{AL}{BK}=1,~\mbox{или}~\frac{AK}{BK}\cdot\frac{BK+AK}{BK}=1.
Обозначив \frac{AK}{BK}=t
, получим уравнение t(1+t)=1
, или t^{2}+t-1=0
, корнем которого является отношение стороны правильного пятиугольника к его диагонали (см. задачу 4197).
Автор: Заславский А. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2017, XIII, финальный тур, № 1, 9 класс
