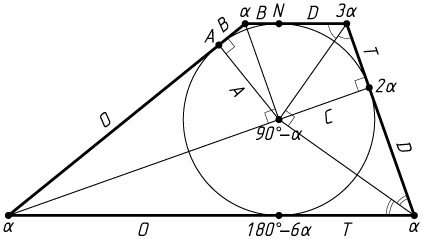
10442. Окружность, вписанная в трапецию ABCD
, касается её боковых сторон AB
и CD
в точках M
и N
соответственно. При этом AM=8MB
и DN=2CN
.
а) Докажите, что AD=4BC
.
б) Найдите MN
, если радиус окружности равен \sqrt{6}
.
Ответ. 4.
Решение. а) Пусть O
— центр окружности, r
— радиус, K
и L
— точки касания окружности с основаниями BC
и AD
соответственно. Положим BM=x
, AM=8x
, CN=y
, DN=2y
. Поскольку CO
и DO
— биссектрисы углов C
и D
трапеции, треугольник COD
прямоугольный (см. задачу 313), а ON
— его высота, проведённая из вершины прямого угла. Значит, CN\cdot DN=ON^{2}
(см. задачу 2728), или 2y^{2}=r^{2}
. Аналогично из прямоугольного треугольника AOB
получаем, что 8x^{2}=r^{2}
. Тогда 2y^{2}=8x^{2}
, y=2x
,
AD=AL+DL=AM+DN=8x+2y=8x+4x=12x,
BC=BK+KC=BM+CN=x+y=x+2x=3x.
Следовательно, AD=4BC
.
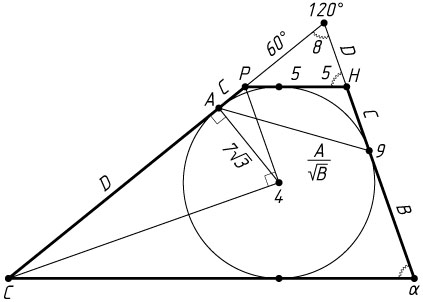
б) Пусть прямые AB
и CD
пересекаются в точке P
. Треугольник BPC
подобен треугольнику APD
с коэффициентом \frac{BC}{AD}=\frac{1}{4}
, поэтому \frac{PC}{PD}=\frac{1}{4}
. Тогда PC=\frac{1}{3}CD=y=2x
. Аналогично находим, что BP=\frac{1}{3}AB=3x
, а так как BC=3x
, то треугольник BPC
равнобедренный.
Пусть \angle APD=\alpha
. Тогда
\cos\alpha=\frac{\frac{1}{2}PC}{BP}=\frac{x}{3x}=\frac{1}{3},
а так как PN=PM=3x+x=4x
, то по теореме косинусов
MN=\sqrt{PM^{2}+PN^{2}-2PM\cdot PN\cos\alpha}=\sqrt{16x^{2}+16x^{2}-2\cdot4x\cdot4x\cdot\frac{1}{3}}=\frac{8x}{\sqrt{3}}.
Из равенства
8x\cdot x=AM\cdot MB=OM^{2}=r^{2}=6,
находим, что x=\frac{\sqrt{3}}{2}
. Следовательно,
MN=\frac{8x}{\sqrt{3}}=4.
Источник: ЕГЭ. — 2017

