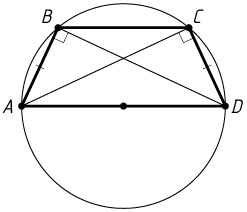
10510. В трапеции ABCD
с основаниями BC
и AD
углы ABD
и ACD
прямые.
а) Докажите, что AB=CD
.
б) Найдите AD
, если AB=2
, BC=7
.
Ответ. 8
.
Решение. а) Из точек B
и C
, лежащих по одну сторону от прямой AD
, отрезок AD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AD
. Трапеция ABCD
вписана в окружность, поэтому она равнобокая. Следовательно, AB=CD
.
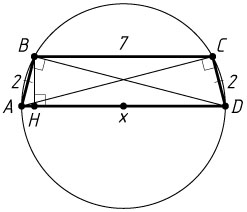
б) Обозначим AD=x
. Пусть BH
— высота трапеции. Тогда
AH=\frac{AD-BC}{2}=\frac{x-7}{2}
(см. задачу 1921), а так как BH
— высота прямоугольного треугольника ABD
, проведённая из вершины прямого угла, то
AB^{2}=AH\cdot AD,~\mbox{или}~4=\frac{x-7}{2}\cdot x
(см. задачу 2728). Из этого уравнения находим, что x=8
.
Источник: ЕГЭ. — 2018, 1 июня

