1052. Дан треугольник ABC
, причём AB=AC
и \angle A=80^{\circ}
. Внутри треугольника ABC
взята такая точка M
, что \angle MBC=30^{\circ}
, а \angle MCB=10^{\circ}
. Найдите \angle AMC
.
Ответ. 70^{\circ}
.
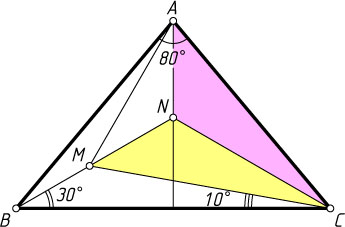
Указание. Пусть N
— точка пересечения прямой BM
с биссектрисой угла BAC
. Докажите, что треугольники ACN
и MCN
равны.
Решение. Первый способ. Пусть N
— точка пересечения прямой BM
с биссектрисой угла BAC
(рис. 1). Поскольку \angle BNC=120^{\circ}
, то
\angle ANC=\angle ANB=120^{\circ},
а так как
\angle ACB=\angle ABC=50^{\circ},~\angle ACN=\angle ABN=20^{\circ},
то
\angle NCM=50^{\circ}-20^{\circ}-10^{\circ}=20^{\circ}.
Поэтому треугольники ACN
и MCN
равны по стороне (CN
— общая) и двум прилежащим к ней углам. Следовательно,
AC=CM,~\angle AMC=\angle MAC=\frac{1}{2}(180^{\circ}-\angle ACM)=
=\frac{1}{2}(180^{\circ}-40^{\circ})=70^{\circ}.
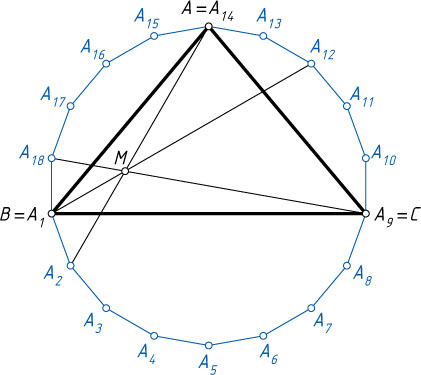
Второй способ. Рассмотрим правильный восемнадцатиугольник A_{1}\dots A_{18}
(рис. 2). Его диагонали A_{1}A_{12}
, A_{2}A_{14}
и A_{9}A_{18}
пересекаются в одной точке (см. задачу 3269). Обозначим её M
, а вершины A_{14}
, A_{1}
и A_{9}
переобозначим как A
, B
и C
соответственно.
Опишем окружность вокруг правильного восемнадцатиугольника A_{1}\dots A_{18}
. Градусные меры дуг с концами в соседних вершинах равны \frac{360^{\circ}}{18}=20^{\circ}
, поэтому
\angle BAC=\angle A_{1}A_{14}A_{9}=80^{\circ},
\angle ABC=\angle A_{14}A_{1}A_{9}=50^{\circ},
\angle BCA=\angle A_{1}A_{9}A_{14}=50^{\circ},
\angle MBC=\angle A_{12}A_{1}A_{9}=30^{\circ},~\angle MCB=\angle A_{1}A_{9}A_{18}=10^{\circ}.
Значит, треугольник ABC
и точка M
удовлетворяют условию задачи.
Хорды A_{2}A_{14}
и A_{9}A_{18}
окружности, описанной около правильного восемнадцатиугольника A_{1}\dots A_{18}
, пересекаются в точке M
, следовательно,
\angle AMC=\angle A_{14}MA_{9}=\frac{\smile A_{14}A_{12}A_{9}+\smile A_{2}A_{1}A_{18}}{2}=
=\frac{100^{\circ}+40^{\circ}}{2}=70^{\circ}
(см. задачу 26).
Третий способ. Пусть O
— центр описанной окружности тупоугольного треугольника BMC
. Центральный угол вдвое больше соответствующего вписанного, поэтому
\angle BOM=20^{\circ},~\angle COM=60^{\circ}.
Значит, равнобедренный треугольник BOC
— равносторонний, поэтому CM=OB=OC
.
Пусть H
— точка пересечения OA
и BC
. Тогда прямая OH
— серединный перпендикуляр к отрезку BC
, а так как
\angle CAO=\frac{1}{2}\angle BAC=40^{\circ}~\mbox{и}~\angle AOC=\frac{1}{2}\angle BOC=40^{\circ},
то треугольник ACO
равнобедренный. Значит, AC=OC=CM
, т. е. треугольник ACM
также равнобедренный. Следовательно,
\angle AMC=\angle CAM=\frac{1}{2}(180^{\circ}-\angle ACM)=\frac{1}{2}(180^{\circ}-(50^{\circ}-10^{\circ}))=70^{\circ}.
Примечание. 1. См. статью Д.Изаака «Выручает описанная окружность», Квант, 1987, N2, с.41-42.
2. См. статью В.Прасолова «Диагонали правильного 18-угольника», Квант, 1995, N5, с.40-42.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1975, № 2, вариант 4
Источник: Журнал «Квант». — 1987, № 2, с. 41, пример 3
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 251(а), с. 30
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 251(а), с. 29
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 12.58, с. 305
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.60, с. 293
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — № 26, с. 259, с. 467
Источник: Всесибирская физико-математическая олимпиада. — 2018-2010, второй этап, задача 3, 9 класс

