1060. В равнобедренном треугольнике ABC
угол при вершине B
равен 20^{\circ}
. На боковых сторонах AB
и CB
взяты соответственно точки Q
и P
, причём \angle QCA=60^{\circ}
, а \angle PAC=50^{\circ}
. Найдите \angle QPA
.
Ответ. 80^{\circ}
.
Указание. Через точку Q
проведите прямую, параллельную стороне AC
.
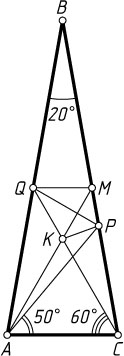
Решение. Первый способ. Через точку Q
проведём прямую, параллельную AC
, до пересечения со стороной BC
в точке M
(рис. 1). Пусть отрезки AM
и CQ
пересекаются в точке K
. Тогда треугольники QMK
и AKC
— равносторонние.
Поскольку
\angle APC=180^{\circ}-50^{\circ}-80^{\circ}=50^{\circ},
то треугольник ACP
— равнобедренный. Поэтому PC=AC=CK
. Следовательно, треугольник KCP
также равнобедренный. Поэтому
\angle QKP=180^{\circ}-80^{\circ}=100^{\circ},
а так как \angle QMC=100^{\circ}
, то
\angle KMP=100^{\circ}-60^{\circ}=40^{\circ},~\angle MKP=100^{\circ}-60^{\circ}=40^{\circ},
т. е. треугольник MPK
— равнобедренный, MP=KP
. Следовательно, треугольники QMP
и QKP
равны по трём сторонам. Поэтому
\angle KQP=\angle MQP=30^{\circ},~\angle QPK=180^{\circ}-100^{\circ}-30^{\circ}=50^{\circ},
\angle APK=\angle CPK-\angle CPA=80^{\circ}-50^{\circ}=30^{\circ}.
Следовательно,
\angle QPA=\angle QPK+\angle APK=50^{\circ}+30^{\circ}=80^{\circ}.
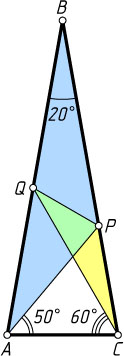
Второй способ. Докажем, что треугольники ABP
и QCP
подобны (рис. 2). Поскольку \angle ABP=\angle QCP=20^{\circ}
, то достаточно проверить, что \frac{AB}{QC}=\frac{BP}{PC}
.
Пусть AB=a
. Тогда из равнобедренного треугольника CQB
находим, что QC=\frac{a}{2\cos20^{\circ}}
. С другой стороны, так как PC=AC
(\angle PAC=\angle APC=50^{\circ}
), то
PC=2a\sin10^{\circ},~BP=BC-PC=a-2a\sin10^{\circ}.
Следовательно, осталось доказать, что
\frac{a}{\frac{a}{2\cos20^{\circ}}}=\frac{a-2a\sin10^{\circ}}{2a\sin10^{\circ}},~\mbox{или}~\sin10^{\circ}\cos20^{\circ}=\frac{1-2\sin10^{\circ}}{4}.
Действительно,
\sin10^{\circ}\cos20^{\circ}=\frac{1}{2}(\sin30^{\circ}-\sin10^{\circ})=
=\frac{1}{2}\left(\frac{1}{2}-\sin10^{\circ}\right)=\frac{1}{4}(1-2\sin10^{\circ}).
Таким образом, треугольники ABP
и QCP
подобны. Следовательно,
\angle CPQ=\angle BPA=180^{\circ}-30^{\circ}-20^{\circ}=130^{\circ},
\angle QPA=\angle CPQ-\angle CPA=130^{\circ}-50^{\circ}=80^{\circ}.
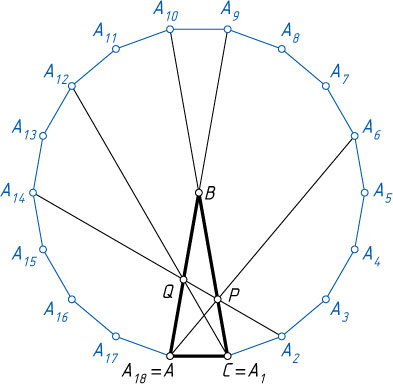
Третий способ. Рассмотрим правильный восемнадцатиугольник A_{1}\dots A_{18}
с центром B
(рис. 3). Его диагонали A_{1}A_{12}
, A_{2}A_{14}
и A_{9}A_{18}
пересекаются в одной точке (см. задачу 3269). Обозначим её Q
. Диагонали A_{2}A_{14}
и A_{6}A_{18}
симметричны относительно A_{1}A_{10}
, значит, они пересекаются в точке P
, лежащей на диагонали A_{1}A_{10}
. Переобозначим вершины A_{18}
и A_{1}
как A
и C
соответственно.
Опишем окружность вокруг правильного восемнадцатиугольника A_{1}\dots A_{18}
. Градусные меры дуг с концами в соседних вершинах равны \frac{360^{\circ}}{18}=20^{\circ}
, поэтому
\angle ABC=\angle A_{1}BA_{18}=20^{\circ},~\angle ACB=\angle BAC=80^{\circ},
\angle PAC=\angle A_{6}A_{18}A_{1}=50^{\circ},~\angle QCA=\angle A_{18}A_{1}A_{12}=60^{\circ}.
Значит, треугольник ABC
и точки P
и Q
удовлетворяют условию задачи.
Хорды A_{6}A_{18}
и A_{2}A_{14}
окружности, описанной около правильного восемнадцатиугольника A_{1}\dots A_{18}
, пересекаются в точке P
, следовательно,
\angle QPA=\angle A_{18}PA_{14}=\frac{\smile A_{18}A_{16}A_{14}+\smile A_{6}A_{4}A_{2}}{2}=
=\frac{80^{\circ}+80^{\circ}}{2}=80^{\circ}
(см. задачу 26).
Примечание. 1. См. также статью В.Прасолова «Диагонали правильного 18-угольника», Квант, 1995, N5, с.40-42.
2. См. также статью К.Кнопа: «История с геометрией, или девять решений одной задачи», Квант, 1993, N11/12, с.47-52.
Источник: Вступительный экзамен в МФТИ. — 1956, билет 3, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 56-3-4, с. 54
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 4, с. 38
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 253, с. 30
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 253, с. 29
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 12.59, с. 305
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.61, с. 293


