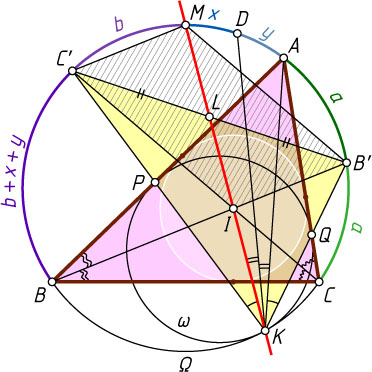
10684. Окружность \omega
касается сторон AB
и AC
треугольника ABC
и касается его описанной окружности \Omega
в точке K
. Пусть I
— центр вписанной окружности треугольника ABC
, M
— середина дуги BC
, не содержащей точки K
. Докажите, что точки K
, I
и M
лежат на одной прямой.
Решение. Без ограничения общности будем считать, что AB\gt AC
.
Пусть биссектрисы углов ABC
, ACB
и B'KC'
пересекают описанную окружность треугольника ABC
в точках B'
C'
и D
соответственно. Тогда B'
, C'
и D
— середины меньших дуг соответственно AC
, AB
и B'C'
.
Пусть окружность \omega
касается сторон AB
и AC
в точках P
и Q
соответственно. Тогда по лемме Архимеда для сегмента (см. задачу 89) точки P
и Q
лежат на отрезках KC'
и KB'
соответственно. Следовательно, KA
— симедиана треугольника QKP
(см. задачу 10449).
При гомотетии с центром K
и коэффициентом \frac{KC'}{KP}
окружность \omega
переходит в описанную окружность треугольника B'KC'
, т. е. в окружность \Omega
. При этом симедиана KA
треугольника QKP
переходит в симедиану треугольника B'KC'
.
Обозначим
\smile AB'=\smile CB'=a,~\smile C'M=b,~\smile AD=x,~\smile DM=y.
Поскольку C'
и M
— середины дуг AC'B
и BMC
, то
\smile BM=\smile BC'+\smile C'M=(b+x+y)+b=2b+x+y,
\smile CM=2a+x+y,
а так как \smile BM=\smile CM
, то a=b
. Из равенства дуг C'D
и B'D
следует, что b+y=a+x
, откуда x=y
. Из равенства дуг C'M
и CB'
получаем MB'\parallel CC'
(см. примечание к задаче 1678). Аналогично докажем, что MC'\parallel BB'
.
Биссектрисы BB'
и CC'
пересекаются в точке I
, и MB'IC'
— параллелограмм. Точка L
пересечения его диагоналей — середина стороны B'C'
треугольника B'KC'
, а KL
— медиана этого треугольника. В то же время, при симметрии относительно биссектрисы KD
, луч KA
перейдёт в луч KM
. Значит, поскольку KA
— симедиана, то луч KM
содержит медиану KL
. Следовательно, точки K
, M
и I
лежат на одной прямой. Что и требовалось доказать.