1070. В равнобедренном треугольнике ABC
с основанием AC
угол при вершине B
равен 100^{\circ}
. Точка D
внутри треугольника ABC
такова, что \angle DAC=20^{\circ}
, \angle DCA=30^{\circ}
. Найдите \angle ADB
.
Ответ. 80^{\circ}
.
Указание. Поместите треугольник ABC
внутрь равностороннего треугольника AEC
. Тогда треугольники ABE
и ADC
равны.
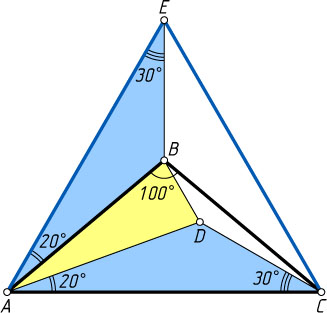
Решение. Первый способ. Поместим треугольник ABC
внутрь равностороннего треугольника AEC
(рис. 1). Тогда
\angle BAE=60^{\circ}-\angle BAC=60^{\circ}-40^{\circ}=20^{\circ},~\angle BEA=\frac{1}{2}\angle AEC=30^{\circ},
поэтому треугольники ABE
и ADC
равны по стороне и двум прилежащим к ней углам. Значит, AB=AD
, поэтому треугольник ABD
равнобедренный, а так как \angle BAD=20^{\circ}
, то
\angle ADB=\frac{1}{2}(180^{\circ}-\angle BAD)=
=90^{\circ}-10^{\circ}=80^{\circ}.
Второй способ. Лемма. Диагонали A_{1}A_{7}
, A_{3}A_{15}
и A_{5}A_{18}
правильного восемнадцатиугольника A_{1}\dots A_{18}
пересекаются в одной точке.
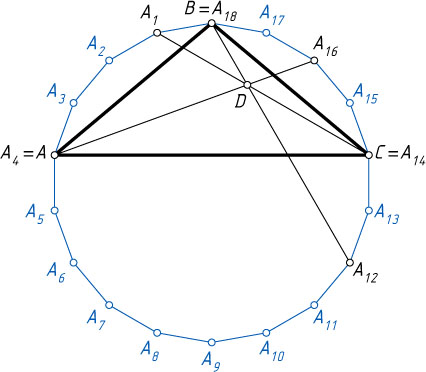
Доказательство. Опишем окружность вокруг правильного восемнадцатиугольника (рис. 2). Градусные меры дуг с концами в соседних вершинах равны \frac{360^{\circ}}{18}=20^{\circ}
, значит,
\angle A_{1}A_{5}A_{18}=\frac{1}{2}\smile A_{1}A_{18}=\frac{1}{2}\cdot20^{\circ}=10^{\circ}.
Аналогично находим, что
\angle A_{18}A_{5}A_{15}=30^{\circ},
\angle A_{5}A_{15}A_{3}=20^{\circ},
\angle A_{3}A_{15}A_{1}=20^{\circ},
\angle A_{7}A_{1}A_{15}=80^{\circ},~\angle A_{5}A_{1}A_{7}=10^{\circ}.
Тогда
\frac{\sin\angle A_{1}A_{5}A_{18}}{\sin\angle A_{18}A_{5}A_{15}}\cdot\frac{\sin\angle A_{5}A_{15}A_{3}}{\sin\angle A_{3}A_{15}A_{1}}\cdot\frac{\sin\angle A_{7}A_{1}A_{15}}{\sin\angle A_{5}A_{1}A_{7}}=
=\frac{\sin10^{\circ}}{\sin30^{\circ}}\cdot\frac{\sin20^{\circ}}{\sin20^{\circ}}\cdot\frac{\sin80^{\circ}}{\sin10^{\circ}}=
=\frac{2\sin80^{\circ}\sin10^{\circ}}{\sin20^{\circ}}=
=\frac{2\sin80^{\circ}\sin10^{\circ}}{\sin20^{\circ}}=\frac{2\cos10^{\circ}\sin10^{\circ}}{\sin20^{\circ}}=1.
Применяя тригонометрическую форму теоремы Чевы к треугольнику A_{1}A_{5}A_{15}
, получим, что прямые A_{1}A_{7}
, A_{5}A_{18}
и A_{15}A_{3}
пересекаются в одной точке (см. задачу 1900). Лемма доказана.
Переобозначим вершины A
, B
, C
треугольника ABC
буквами A_{15}
, A_{1}
и A_{5}
соответственно. Тогда по лемме D
— точка пересечения диагоналей A_{1}A_{7}
, A_{5}A_{18}
и A_{15}A_{3}
правильного восемнадцатиугольника A_{1}\dots A_{18}
. Следовательно,
\angle ADB=\angle A_{15}DA_{1}=\frac{1}{2}(\smile A_{1}A_{18}A_{15}+\smile A_{3}A_{5}A_{7})=
=\frac{1}{2}(80^{\circ}+80^{\circ})=80^{\circ}
(см. задачу 26).
Примечание. См. статью В.Прасолова «Диагонали правильного 18-угольника», Квант, 1995, N5, с.40-42.
Источник: Шень А. Х. Геометрия в задачах. — М.: МЦНМО, 2013. — № 277, с. 79
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 312, с. 49

