10874. Пусть высоты AA_{1}
и BB_{1}
остроугольного неравнобедренного треугольника ABC
пересекаются в точке H
, M
— середина стороны AB
, \omega
и \omega_{1}
— окружности, описанные около треугольников ABC
и A_{1}B_{1}C
соответственно, а P
— вторая точка их пересечения. Докажите, что:
а) окружности, описанные около треугольников AMA_{1}
и BMB_{1}
, проходят через точку P
;
б) PM
— биссектриса углов A_{1}PA
и B_{1}PB
;
в) прямая PA
проходит через точку, симметричную точке A_{1}
относительно прямой CH
.
Решение. а) Точки M
, H
и P
лежат на одной прямой (см. задачу 3180), поэтому
\angle A_{1}PM=\angle A_{1}PH=\angle A_{1}CH=90^{\circ}-\angle ABC=\angle HAM=\angle A_{1}AM.
Следовательно, окружность, описанная около треугольника AMA_{1}
проходит через точку P
. Аналогично для описанной окружности треугольника BMB_{1}
.
б) Отрезок A_{1}M
— медиана прямоугольного треугольника AA_{1}B
, проведённая из вершины прямого угла, поэтому A_{1}M=AM
(см. задачу 1109). По доказанному в предыдущем пункте, точка P
лежит на описанной окружности треугольника AMA_{1}
, а углы APM
и A_{1}PM
вписаны в эту окружность и опираются на равные хорды AM
и A_{1}M
. Следовательно, они равны, т. е. PM
— биссектриса угла A_{1}PA
. Аналогично, PM
— биссектриса угла B_{1}PB
.
в) Пусть луч PA
пересекает вторично окружность \omega_{1}
в точке A_{2}
. По доказанному в предыдущем пункте, PM
— биссектриса угла A_{1}PA
, поэтому дуги HA_{1}
и HA_{2}
окружности \omega_{1}
равны. Значит, точки A_{1}
и A_{2}
симметричны относительно диаметра CH
этой окружности.
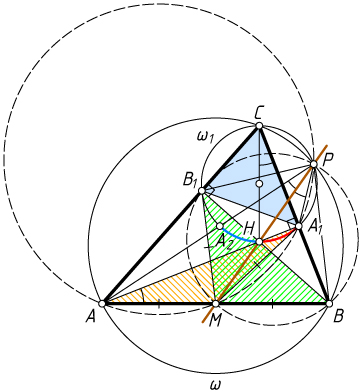
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Источник: Журнал «Квант». — 2014, № 1, с. 43
