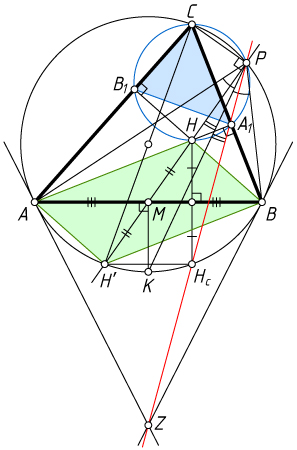
10879. Пусть высоты AA_{1}
и BB_{1}
неравнобедренного остроугольного треугольника ABC
пересекаются в точке H
, H_{c}
— точка, симметричная точке H
относительно стороны AB
, P
— вторая точка пересечения описанных окружностей треугольников ABC
и A_{1}B_{1}C
, Z
— точка пересечения касательных к описанной окружности треугольника ABC
, проведённых в точках A
и B
. Докажите, что точки Z
, P
и H_{c}
лежат на одной прямой.
Решение. Согласно основному свойству симедианы, PZ
— симедиана треугольника PAB
(см. задачу 10449). Остаётся доказать, что точка H_{c}
также лежит на симедиане.
Точки P
, H
и середина M
стороны BC
лежат на одной прямой (см. задачу 3180). Пусть эта прямая второй раз пересекает описанную окружность треугольника ABC
в точке H'
. Тогда CH'
— диаметр описанной окружности треугольника ABC
, а точка H'
симметрична H
относительно точки M
(см. задачу 6300).
Пусть серединный перпендикуляр к стороне AB
пересекает дугу AH_{c}B
в точке K
. Тогда K
— середина этой дуги, а PK
— биссектриса угла APB
. Поскольку H'H_{c}\parallel AB
, а дуги, заключённые между параллельными хордами, равны, то K
— середина дуги H'H_{c}
. Значит, PK
— биссектриса угла H'PH_{c}
. Следовательно, луч PH'
, содержащий медиану PM
треугольника APB
, симметричен лучу PH_{c}
относительно биссектрисы угла APB
, т. е. луч PH_{c}
лежит на симедиане треугольника APB
. Что и требовалось доказать.
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Блинков Ю. А.
Источник: Журнал «Квант». — 2014, № 1, с. 45
