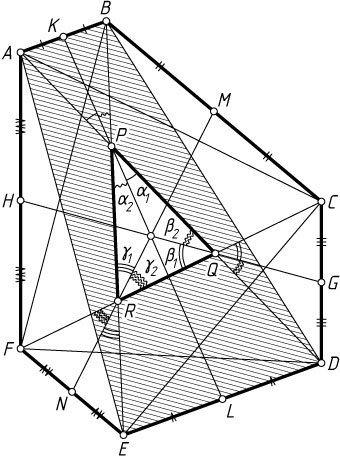
1089. Противоположные стороны выпуклого шестиугольника попарно параллельны. Докажите, что прямые, соединяющие середины противоположных сторон, пересекаются в одной точке.
Указание. Примените теорему Чевы в тригонометрической форме (см. задачу 1900) к треугольнику, образованному пересечениями диагоналей шестиугольника, соединяющими его противоположные вершины.
Решение. Пусть ABCDEF
— данный шестиугольник, K
, M
, G
, L
, N
и H
— середины его сторон AB
, BC
, CD
, DE
, EF
и AF
соответственно, P
— точка пересечения диагоналей AD
и BE
, Q
— точка пересечения диагоналей AD
и CF
, R
— диагоналей BE
и CF
.
Поскольку ABDE
— трапеция или параллелограмм, отрезок KL
, соединяющий середины сторон AB
и ED
, проходит через точку P
(см. задачу 1513).
Обозначим
\angle APK=\angle DPL=\alpha_{1},~\angle KPB=\angle LPE=\alpha_{2},
\angle CQG=\angle FQH=\beta_{1},~\angle GQD=\angle HQA=\beta_{2},
\angle ERN=\angle BRM=\gamma_{1},~\angle NRF=\angle MRC=\gamma_{2}.
Применяя теорему синусов к треугольникам APK
и BPK
, получим, что
\frac{\sin\alpha_{1}}{\sin\angle AKP}=\frac{AK}{AP},~\frac{\sin\alpha_{2}}{\sin\angle BKP}=\frac{BK}{BP},
а так как \sin\angle AKP=\sin\angle BKP
, AK=BK
и AB\parallel DE
, то
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}=\frac{BP}{AP}=\frac{BE}{AD}.
Аналогично
\frac{\sin\beta_{1}}{\sin\beta_{2}}=\frac{AD}{CF},~\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=\frac{CF}{BE}.
Перемножая три этих равенства, получим, что
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=\frac{BE}{AD}\cdot\frac{AD}{CF}\cdot\frac{CF}{BE}=1.
Следовательно, по теореме Чевы (в тригонометрической форме), применённой к треугольнику, образованному пересечениями прямых AD
, BE
и CF
, прямые KL
, MN
и GH
пересекаются в одной точке. Что и требовалось доказать.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.80, с. 115
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.98, с. 113
