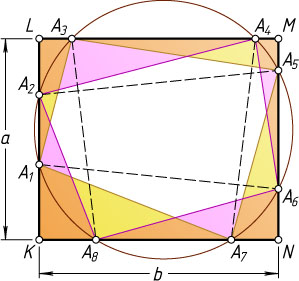
11267. Окружность пересекает стороны прямоугольника в восьми точках, которые последовательно занумерованы. Докажите, что площадь четырёхугольника с вершинами в точках с нечётными номерами равна площади четырёхугольника с вершинами в точках с чётными номерами.
Решение. Рассмотрим отрезки LA_{3}
, MA_{4}
и KA_{8}
, NA_{7}
горизонтальных сторон LM
и KN
прямоугольника KLMN
(см. рис.). Вписанный четырёхугольник A_{3}A_{4}A_{7}A_{8}
— либо равнобедренная трапеция (см. задачу 5003), либо прямоугольник. В первом случае проекции боковых сторон на большее основание равны полуразности оснований (см. задачу 1021), поэтому
LA_{3}-KA_{8}=MA_{4}-NA_{7},~\mbox{или}~LA_{3}+NA_{7}=MA_{4}+KA_{8}.
Во втором случае эти равенства очевидны. Аналогично получаем другое вспомогательное равенство для отрезков вертикальных сторон:
KA_{1}+MA_{5}=LA_{2}+NA_{6}.
Обозначим KL=MN=a
, KN=LM=b
.
Докажем, что сумма площадей четырёх прямоугольных треугольников LA_{1}A_{3}
, NA_{5}A_{7}
, KA_{7}A_{1}
и MA_{3}A_{5}
равна сумме площадей треугольников MA_{6}A_{4}
, KA_{2}A_{8}
, LA_{4}A_{2}
и NA_{8}A_{6}
, т. е.
S_{\triangle LA_{1}A_{3}}+S_{\triangle NA_{5}A_{7}}+S_{\triangle KA_{7}A_{1}}+S_{\triangle MA_{3}A_{5}}=
=S_{\triangle MA_{6}A_{4}}+S_{\triangle KA_{2}A_{8}}+S_{\triangle LA_{4}A_{2}}+S_{\triangle NA_{6}A_{8}}.
Действительно,
S_{\triangle LA_{1}A_{3}}+S_{\triangle NA_{5}A_{7}}+S_{\triangle KA_{7}A_{1}}+S_{\triangle MA_{3}A_{5}}=
=S_{\triangle MA_{6}A_{4}}+S_{\triangle KA_{2}A_{8}}+S_{\triangle LA_{4}A_{2}}+S_{\triangle NA_{6}A_{8}}~\Leftrightarrow
\Leftrightarrow~\frac{1}{2}LA_{1}\cdot LA_{3}+\frac{1}{2}NA_{5}\cdot NA_{7}+\frac{1}{2}KA_{1}\cdot KA_{7}+\frac{1}{2}MA_{5}\cdot MA_{3}=
=\frac{1}{2}MA_{4}\cdot MA_{6}+\frac{1}{2}KA_{2}\cdot KA_{8}+\frac{1}{2}LA_{2}\cdot LA_{4}+\frac{1}{2}NA_{6}\cdot NA_{8}~\Leftrightarrow
\Leftrightarrow~LA_{3}(b-KA_{1})+NA_{7}(b-MA_{5})+KA_{1}(a-NA_{7})+MA_{5}(a-LA_{3})=
=MA_{4}(b-NA_{6})+KA_{8}(b-LA_{2})+LA_{2}(a-MA_{4})+NA_{6}(a-KA_{8})~\Leftrightarrow
\Leftrightarrow~b(LA_{3}+NA_{7})+a(KA_{1}+MA_{5})-
-LA_{3}\cdot KA_{1}-NA_{7}\cdot MA_{5}-KA_{1}\cdot NA_{7}-MA_{5}\cdot LA_{3}=
=b(MA_{4}+KA_{8})+a(LA_{2}+NA_{6})-
-MA_{4}\cdot NA_{6}-KA_{8}\cdot LA_{2}-LA_{2}\cdot MA_{4}-NA_{6}\cdot KA_{8}~\Leftrightarrow
\Leftrightarrow~LA_{3}\cdot KA_{1}+NA_{7}\cdot MA_{5}+KA_{1}\cdot NA_{7}+MA_{5}\cdot LA_{3}=
=MA_{4}\cdot NA_{6}+KA_{8}\cdot LA_{2}+LA_{2}\cdot MA_{4}+NA_{6}\cdot KA_{8}~\Leftrightarrow
\Leftrightarrow~KA_{1}(LA_{3}+NA_{7})+MA_{5}(NA_{7}+LA_{3})=
=MA_{4}(NA_{6}+LA_{2})+KA_{8}(LA_{2}+NA_{6})~\Leftrightarrow
\Leftrightarrow~(LA_{3}+NA_{7})(KA_{1}+MA_{5})=(LA_{2}+NA_{6})(MA_{4}+KA_{8}).
Последнее равенство верно, так как по доказанному
LA_{3}+NA_{7}=MA_{4}+KA_{8}~\mbox{и}~KA_{1}+MA_{5}=LA_{2}+NA_{6}.
Из доказанного равенства сумм площадей следует, что площади четырёхугольников A_{1}A_{3}A_{5}A_{7}
и A_{2}A_{4}A_{6}A_{8}
также равны.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 1999, № 6, с. 13, М1709; 2000, № 3, с. 27, М1709
Источник: Задачник «Кванта». — М1709
