1206. С помощью циркуля и линейки постройте пятиугольник по серединам его сторон.
Указание. Середины трёх последовательных сторон пятиугольника и середина одной из его диагоналей являются вершинами параллелограмма.
Решение. Первый способ. Предположим, что задача решена. Пусть M_{1}
, M_{2}
, M_{3}
, M_{4}
, M_{5}
— середины последовательных сторон A_{1}A_{2}
, A_{2}A_{3}
, A_{3}A_{4}
, A_{4}A_{5}
, A_{1}A_{5}
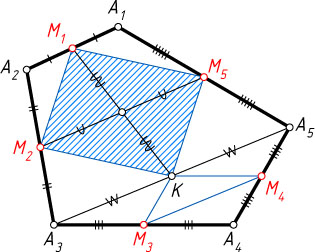
искомого пятиугольника. Если K
— середина диагонали A_{3}A_{5}
, то четырёхугольник M_{1}M_{2}KM_{5}
— параллелограмм (см. задачу 1204).
Построение: находим точку K
; строим треугольник A_{3}A_{4}A_{5}
по серединам его сторон M_{3}
, M_{4}
и K
; построенный треугольник достраиваем до искомого пятиугольника.
Второй способ. Композиция симметрий относительно середин последовательных сторон пятиугольника есть центральная симметрия (см. задачу 6710).
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 117, с. 106
