12075. В треугольнике ABC
через середину K
биссектрисы BD
проведена прямая, перпендикулярная BD
и пересекающая прямую AC
в точке E
. Докажите, что DE^{2}=AE\cdot EC
.
Указание. Треугольники BCE
и ABE
подобны.
Решение. Первый способ. Точка E
лежит на серединном перпендикуляре к отрезку BD
, значит, DE=BE
. Углы при основании BD
равнобедренного треугольника BDE
равны, а BDE
— внешний угол треугольника ABD
, поэтому
\angle BAE=\angle BDE-\angle ABD=\angle DBE-\angle CBD=\angle CBE.
Значит, треугольник BCE
подобен треугольнику ABE
по двум углам. Тогда \frac{BE}{AE}=\frac{EC}{BE}
. Следовательно,
DE^{2}=BE^{2}=AE\cdot EC.
Что и требовалось доказать.
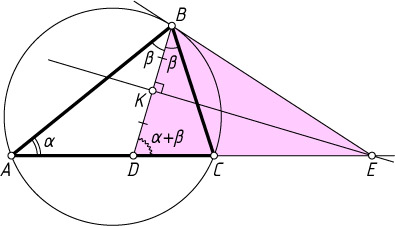
Второй способ. Проведём окружность, описанную около треугольника ABC
, и докажем, что EB
— касательная к ней (см. рисунок). Пусть
\angle BAC=\alpha,~\angle DBA=\angle DBC=\beta.
Тогда по теореме о внешнем угле треугольника
\angle BDE=\angle BDC=\angle BAD+\angle ABD=\alpha+\beta.
Треугольник BED
равнобедренный, так как его высота EK
является медианой, поэтому,
\angle DBE=\angle BDE=\alpha+\beta,
Тогда
\angle CBE=\alpha=\angle BAC.
Значит, EB
— касательная к окружности (см. задачу 144).
Следовательно, по теореме о касательной и секущей (см. задачу 93)
DE^{2}=BE^{2}=AE\cdot EC.
Что и требовалось доказать.
Источник: Международная олимпиада «Интеллектуальный марафон». — 1992, II, задача 7
Источник: Журнал «Квант». — 1993, № 2, с. 82, задача 7
Источник: Московская математическая регата. — 2019-2020, второй тур, № 2, 11 класс
