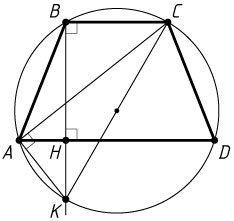
12144. Трапеция ABCD
с большим основанием AD
и высотой BH
вписана в окружность. Прямая BH
вторично пересекает эту окружность в точке K
.
а) Докажите, что прямые AC
и AK
перпендикулярны.
б) Прямые CK
и AD
пересекаются в точке N
. Найдите AD
, если радиус окружности равен 12, \angle BAC=30^{\circ}
, а площадь четырёхугольника BCNH
в восемь раз больше площади треугольника KNH
.
Ответ. 4\sqrt{33}
.
Решение. а) Прямые BC
и AD
параллельны, а BH\perp AD
, поэтому \angle KBC=90^{\circ}
. Хорда CK
видна из точки B
, лежащей на окружности, под прямым углом, значит, CK
— диаметр окружности. Точка A
лежит на окружности с диаметром CK
, значит, \angle CAK=90^{\circ}
. Следовательно, AC\perp AK
. Что и требовалось доказать.
б) Вписанные углы BKC
и BAC
опираются на одну и ту же дугу, поэтому
\angle BKC=\angle BAC=30^{\circ}.
Из прямоугольного треугольника BCK
находим, что
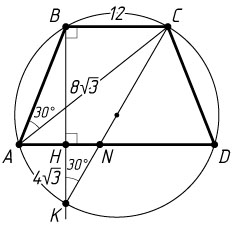
BC=\frac{1}{2}CK=12,~BK=CK\cos\angle BKC=BC\cos30^{\circ}=12\cdot\frac{\sqrt{3}}{2}=12\sqrt{3}.
Площадь четырёхугольника BCNH
в восемь раз больше площади треугольника KNH
, поэтому площадь треугольника BKC
в девять раз больше площади треугольника HKN
, а так как треугольник HKN
подобен треугольнику BKC
, то коэффициент подобия равен \frac{1}{3}
. Значит,
KH=\frac{1}{3}BK=4\sqrt{3},~BH=BK-KH=8\sqrt{3}.
Обозначим AD=x
. Тогда (см. задачу 1921)
AH=\frac{AD-BC}{2}=\frac{x-12}{2},~DH=\frac{AD+BC}{2}=\frac{x+12}{2}.
По теореме о произведении отрезков пересекающихся хорд (см. задачу 2627) AH\cdot DH=KH\cdot BH
, или
\frac{x-12}{2}\cdot\frac{x+12}{2}=4\sqrt{3}\cdot8\sqrt{3},~x^{2}=144+4\cdot32\cdot3,~x^{2}=16(9+24),~x^{2}=16\cdot33.
Следовательно, AD=x=4\sqrt{33}
.
Источник: ЕГЭ. — 2021, задача 16

