12169. В окружность радиуса 8 вписана трапеция ABCD
, причём её основание AD
является диаметром, а \angle ABC=120^{\circ}
. Хорда CM
пересекает диаметр AD
в точке P
так, что длина отрезка AP
равна 4.
а) Докажите, что MB
— биссектриса угла AMC
.
б) Найдите площадь треугольника PMD
.
Ответ. \frac{72\sqrt{3}}{7}
.
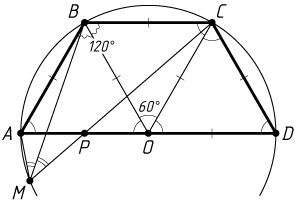
Решение. а) Пусть O
— центр окружности. Тогда AO=OB=8
, а так как \angle BAO=60^{\circ}
, то треугольник AOB
равносторонний. Значит, AB=8
и \angle AOB=60^{\circ}
. Аналогично, CD=8
и \angle COD=60^{\circ}
. Тогда
\angle BOC=180^{\circ}-2\cdot60^{\circ}=60^{\circ}.
Значит, треугольник BOC
тоже равносторонний, поэтому BC=OB=AB
.
Вписанные острые углы AMB
и BMC
опираются на равные хорды, поэтому они равны. Следовательно, MB
— биссектриса угла AMC
. Что и требовалось доказать.
б) Пусть BP'
— высота трапеции. Поскольку трапеция вписана в окружность, она равнобедренная, поэтому (см. задачу 1921)
AP'=\frac{AD-BC}{2}=\frac{16-8}{2}=4=AP.
Значит, точка P'
совпадает с P
, и BP
— высота трапеции.
Из прямоугольных треугольников ABP
и BCP
находим, что
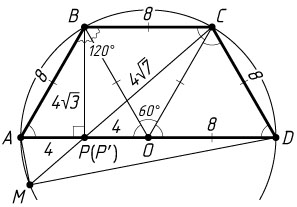
BP=AB\sin60^{\circ}=8\cdot\frac{\sqrt{3}}{2}=4\sqrt{3},
CP=\sqrt{BC^{2}+BP^{2}}=\sqrt{64+48}=4\sqrt{7}.
По теореме о произведениях отрезков пересекающихся хорд CP\cdot PM=AP\cdot DP
, откуда
PM=\frac{AP\cdot DP}{CP}=\frac{4\cdot12}{4\sqrt{7}}=\frac{12}{\sqrt{7}},
поэтому
\frac{PM}{CP}=\frac{\frac{12}{\sqrt{7}}}{4\sqrt{7}}=\frac{3}{7}.
Следовательно (см. задачу 3000),
S_{\triangle PMD}=\frac{PM}{CP}\cdot S_{\triangle PCD}=\frac{3}{7}\cdot\frac{1}{2}DP\cdot BP=\frac{3}{7}\cdot\frac{1}{2}\cdot12\cdot4\sqrt{3}=\frac{72\sqrt{3}}{7}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021, 11 класс, задача 16

