1223. У четырёхугольника нет параллельных сторон. Докажите, что отрезки, соединяющие середины его противоположных сторон, и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся ею пополам.
Указание. Четырёхугольник с вершинами в серединах сторон другого четырёхугольника — параллелограмм (см. задачу 1204).
Решение. Первый способ. Пусть M
, N
, K
, L
— середины сторон соответственно AB
, BC
, CD
, AD
четырёхугольника ABCD
. Поскольку MN
— средняя линия треугольника ABC
, то MN=\frac{1}{2}AC
и MN\parallel AC
. Аналогично докажем, что KL=\frac{1}{2}AC
и KL\parallel AC
. Значит, MN=KL
и MN\parallel KL
. Следовательно, четырёхугольник MNKL
— параллелограмм. Его диагонали KM
и LN
точкой пересечения O
делятся пополам.
Пусть P
и Q
— середины диагоналей AC
и BD
четырёхугольника ABCD
. Тогда MPKQ
— параллелограмм, так как его противоположные стороны MP
и KQ
— средние линии треугольников ABC
и BDC
с общей стороной BC
. Диагональ PQ
этого параллелограмма проходит через середину O
его диагонали MK
и делится точкой O
пополам.
Следовательно, отрезки MK
, LN
и PQ
проходят через точку O
и делятся ею пополам. Что и требовалось доказать.
Второй способ. Пусть X
— произвольная точка плоскости, O_{1}
, O_{2}
и O_{3}
— середины отрезков MK
, LN
и PQ
соответственно. Тогда (см. задачу 4500)
\overrightarrow{XO_{1}}=\frac{1}{2}(\overrightarrow{XM}+\overrightarrow{XK})=\frac{1}{2}\left(\frac{1}{2}(\overrightarrow{XA}+\overrightarrow{XB})+\frac{1}{2}(\overrightarrow{XC}+\overrightarrow{XD})\right)=
=\frac{1}{4}(\overrightarrow{XA}+\overrightarrow{XB}+\overrightarrow{XC}+\overrightarrow{XD}).
Аналогично
\overrightarrow{XO_{2}}=\frac{1}{4}(\overrightarrow{XA}+\overrightarrow{XB}+\overrightarrow{XC}+\overrightarrow{XD}),
\overrightarrow{XO_{3}}=\frac{1}{4}(\overrightarrow{XA}+\overrightarrow{XB}+\overrightarrow{XC}+\overrightarrow{XD}).
Значит, точки O_{1}
, O_{2}
и O_{3}
совпадают. Отсюда следует утверждение задачи.
Третий способ. Пусть M
, N
, K
, L
— середины сторон соответственно AB
, BC
, CD
, AD
четырёхугольника ABCD
, а P
и Q
— середины диагоналей AC
и BD
.
Поместим в вершины четырёхугольника единичные массы. Пусть O
— центр масс материальной системы точек A
, B
, C
и D
. Поместив в точки M
и K
массы 2, получим, что середина отрезка MK
совпадает с O
. Аналогично докажем, что середина отрезка NL
также совпадает с O
. Поместив в точки P
и Q
массы 2, получим, что и середина отрезка PQ
совпадает с O
. Отсюда следует утверждение задачи.
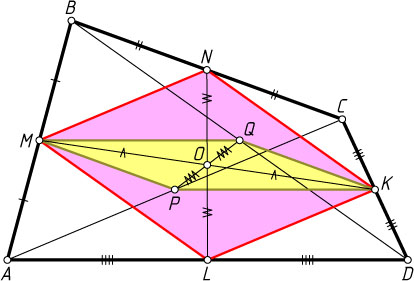
Примечание. Точка пересечения отрезков, соединяющих середины противоположных сторон четырёхугольника, называется центроидом четырёхугольника.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 209, с. 21
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 80; № 1.14, с. 163
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 14.5, с. 326
