12329. В треугольнике ABC
биссектрисы AK
и BL
пересекаются в точке I
. Известно, что около четырёхугольника CKIL
можно описать окружность.
а) Докажите, что \angle BCA=60^{\circ}
.
б) Найдите площадь треугольника ABC
, если его периметр равен 25 и IC=4
.
Ответ. 25.
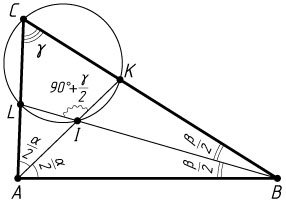
Решение. а) Обозначим \angle ACB=\gamma
. Тогда
\angle KIL=\angle AIB=90^{\circ}+\frac{\gamma}{2}
(см. задачу 4770), а так как четырёхугольник CKIL
вписанный, то
\angle KIL=180^{\circ}-\angle KCL=180^{\circ}-\gamma.
Из равенства
90^{\circ}+\frac{\gamma}{2}=180^{\circ}-\gamma
получаем, что \gamma=60^{\circ}
.
б) Поскольку точка I
— точка пересечения биссектрис AK
и BL
, она также лежит на биссектрисе угла ACB
, и I
—центр вписанной в треугольник ABC
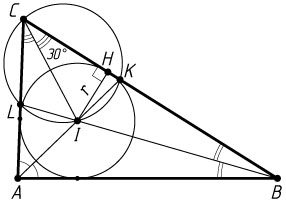
окружности (см. задачу 1140). Значит, радиус r
этой окружности равен перпендикуляру IH
, опущенному из этой точки на сторону BC
. В прямоугольном треугольнике CIH
угол HCI
равен половине угла ACB
, т. е. 30^{\circ}
. Значит,
IH=\frac{1}{2}IC=2.
Площадь треугольника ABC
равна половине произведения его периметра на радиус вписанной окружности (см. 452). Следовательно,
S_{\triangle ABC}=\frac{1}{2}\cdot25r=\frac{1}{2}\cdot25\cdot2=25.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021

