12411. Треугольник скользит по своей плоскости так, что две его стороны всё время проходят через две неподвижные точки. Покажите, что третья сторона сохраняет постоянное расстояние от третьей неподвижной точки.
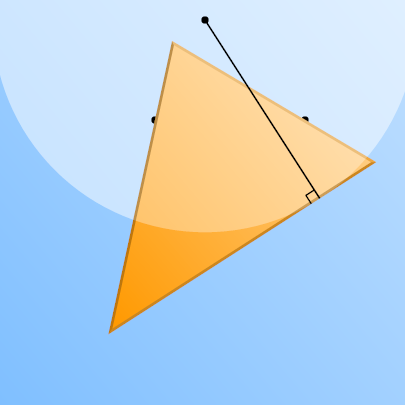
Решение. Обозначим неподвижные точки через A
и B
и допустим, что сторона XY
нашего движущегося треугольника XYZ
проходит через точку A
, а сторона XZ
— через точку B
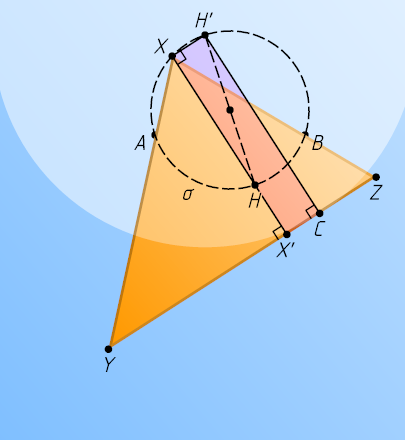
. Поскольку угол \alpha=\angle YXZ
не меняется, то вершина X
лежит на фиксированной окружности \sigma
, проходящей через точки A
и B
(см. задачу 12).
Опустим высоту h=XX'
на сторону YZ
и определим точку H
как пересечение этой высоты и окружности \sigma
. Поскольку
\angle BXH=\angle ZXX'=90^{\circ}-\angle YZX,
угол BXH
всегда один и тот же, поэтому точка H
не меняется при движении треугольника.
Пусть H'
— точка на окружности \sigma
, диаметрально противоположная H
, а H'C
— перпендикуляр, опущенный из точки H'
на прямую YZ
. Тогда \angle H'XX'=\angle H'XH=90^{\circ}
(см. задачу 1689), поэтому H'CX'X
— прямоугольник. Прямая YZ
удалена от точки H'
на расстояние H'C=XX'=h
, которое всегда одно и то же (это длина высоты h
треугольника XYZ
).
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1934, третий тур, задача 1(б), 10 класс
Источник: Журнал «Квант». — 2020, № 7, с. 19

