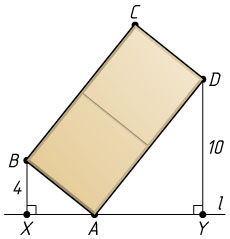
12586. Через вершину A
прямоугольника ABCD
проведена прямая l
, как изображено на рисунке. Из точек B
и D
опущены перпендикуляры BX
и DY
на прямую l
. Найдите XY
, если известно, что BX=4
, DY=10
, BC=2AB
.
Ответ. 13.
Решение. Первый способ. Прямоугольные треугольники AXB
и DYA
подобны, так как
\angle BAX=90^{\circ}-\angle DAY=\angle ADY,
причём коэффициент подобия равен \frac{AB}{DA}=\frac{1}{2}
. Значит,
AX=\frac{1}{2}DY=5,~AY=2BX=8.
Следовательно,
XY=AX+AY=5+8=13.
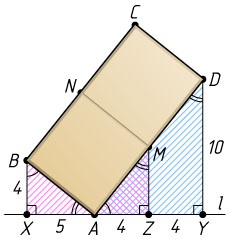
Второй способ. Пусть M
и N
— середины AD
и BC
соответственно, а MZ
— перпендикуляр к прямой l
. Тогда ABNM
— квадрат, а MZ
— средняя линия треугольника ADY
. Следовательно (см. задачи 1880 и 1065),
MZ=\frac{1}{2}DY=5,~ZY=AZ=BX=4~\Rightarrow
\Rightarrow~XY=XZ+ZY=(XA+AZ)+ZY=
=(BX+MZ)+ZY=(4+5)+4=13.
Источник: Всероссийская олимпиада школьников. — 2021-2022, XLVIII, школьный этап, задача 4, 9 класс

