12729. Точка I
— центр вписанной окружности треугольника ABC
. Окружность \omega
с диаметром BI
вторично пересекается с описанной окружностью \Omega
в точке X
. Докажите, что прямые AC
, BX
и касательная к окружности \omega
в точке I
пересекаются в одной точке.
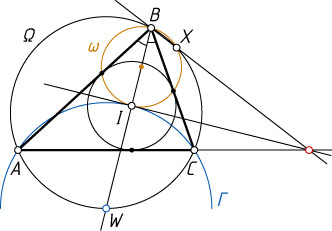
Решение. Пусть луч BI
(биссектриса угла ABC
) пересекает окружность \Omega
в точке W
. Точки A
, I
и C
лежат на окружности \Gamma
с центром W
(см. задачу 788). Поскольку BI+IW=BW
, окружности \omega
и \Gamma
касаются в точке I
. Значит, общая касательная этих окружностей, проведённая в точке I
, — их радикальная ось.
Прямая BX
— радикальная ось окружностей \omega
и \Omega
(см. задачу 6392), а прямая AC
— радикальная ось окружностей \Omega
и \Gamma
. Следовательно, касательная к окружности \omega
в точке I
и прямые BX
и AC
пересекаются в одной точке — радикальном центре этих трёх окружностей (см. задачу 6393).
Источник: Галахова Е. И. Девочка на шаре: Рукопись. — свойство I3, с. 16
