13267. Дан вписанный четырёхугольник ABCD
. На прямых AB
и CD
отмечены точки P
и Q
соответственно, причём описанная окружность треугольника CPD
касается прямой AB
, а описанная окружность треугольника AQB
касается прямой CD
. Докажите, что расстояние от точки P
до прямой CD
равно расстоянию от точки Q
до прямой AB
.
Решение. Если AB\parallel CD
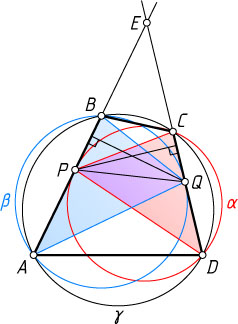
, то утверждение очевидно. Рассмотрим случай, когда прямые AB
и CD
пересекаются в точке E
(см. рис.), а точки P
и Q
лежат на сторонах данного четырёхугольника. Обозначим через \alpha
и \beta
описанные окружности треугольников CPD
и AQB
соответственно, а через \gamma
— описанную окружность четырёхугольника ABCD
.
Тогда степени точки E
относительно окружностей \alpha
и \beta
равны
EP^{2}=EC\cdot ED~\mbox{и}~EQ^{2}=EB\cdot EA
соответственно (см. задачи 2635 и 2636), а степень точки E
относительно окружности \Gamma
равна
EB\cdot EA=EC\cdot ED~\Rightarrow~EQ^{2}=EP^{2}~\Rightarrow~EP=EQ.
Значит, треугольник PEQ
равнобедренный, поэтому его высоты, опущенные на боковые стороны EQ
и EP
, равны. Отсюда следует утверждение задачи.
Аналогично для любого другого случая.
Источник: Журнал «Crux Mathematicorum». — 2020, № 7, задача OC468, с. 298
Источник: Немецкие математические олимпиады. — 2017
