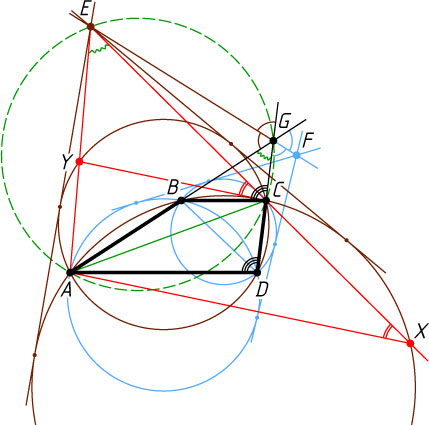
13350. Дана трапеция ABCD
, в которой AD\parallel BC
, а лучи AB
и DC
пересекаются в точке G
. Общие внешние касательные к окружностям, описанным около треугольников ABC
и ACD
, пересекаются в точке E
. Общие внешние касательные к окружностям, описанным около треугольников ABD
и BCD
, пересекаются в точке F
. Докажите, что точки E
, F
и G
лежат на одной прямой.
Решение. Пусть прямая EC
повторно пересекает окружность (ABC)
в точке X
, а прямая EA
повторно пересекает окружность треугольника (ACD)
в точке Y
(рассмотрим случай, изображённый на рисунке; другие случаи рассматриваются аналогично).
Рассмотрим гомотетию с центром E
, переводящую окружность (ABC)
в окружность (ACD)
. При такой гомотетии точка X
переходит в C
, а точка A
— в Y
. Отсюда AX\parallel YC
, и по теореме о внешнем угле треугольника
\angle AEC=\angle AYC-\angle ECY=\angle AYC-\angle AXC.
Поскольку четырёхугольники ABCX
и AYCD
вписанные, то
\angle AXC=180^{\circ}-\angle ABC~\mbox{и}~\angle AYC=180^{\circ}-\angle ADC.
Значит,
\angle AEC=\angle AYC-\angle AXC=180^{\circ}-\angle ADC-(180^{\circ}-\angle ABC)=
=\angle ABC-\angle ADC=\angle ABC-\angle BCG=\angle BGC=\angle AGC
(так как BC\parallel AD
, а ABC
— внешний угол треугольника BCG
). Из полученного равенства следует, что точки A
, C
, E
и G
лежат на одной окружности (см. задачу 12).
Поскольку точка E
лежит на серединном перпендикуляре к отрезку AC
(т. е. на оси симметрии окружностей (ABC)
и (ACD)
), она является серединой дуги AGC
окружности, проходящей через точки A
, C
, E
и G
. Значит, точка E
лежит на внешней биссектрисе угла BGC
.
Аналогично доказывается, что точка F
тоже лежит на внешней биссектрисе угла BGC
. Следовательно, точки E
, F
и G
лежат на одной прямой.
Примечание. У задачи есть следующее обобщение. Пусть ABCD
— четырёхугольник, G
— точка пересечения прямых AB
и CD
, а M
— вторая точка пересечения окружностей (ADG)
и (BCG)
(иначе говоря, точка Микеля этого четырёхугольника, см. задачу 995). Пусть E
— центр гомотетии с положительным коэффициентом, переводящей окружность (ABC)
в окружность (ADC)
. Тогда точки A
, C
, M
, E
лежат на одной окружности, причём E
— середина дуги AC
(т. е. ME
— биссектриса угла между AM
и CM
).
Доказать это можно аналогично решению решении задачи: имеем (в ориентированных углах)
\angle AEC=\angle ABC+\angle ADC=\angle GBC+\angle AMG=
=\angle GMC+\angle AMG=\angle AMC.
Автор: Кузнецов А. С.
Источник: Всероссийская олимпиада школьников. — 2022-2023, XLIX, заключительный этап, второй день, задача 7, 9-10 классы
