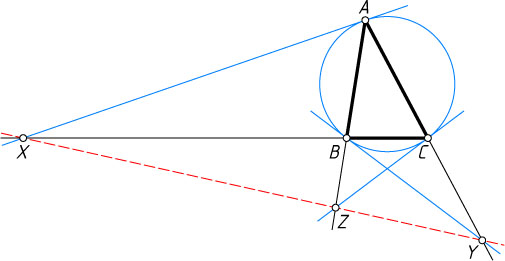
13513. Касательная в точке A
к описанной окружности треугольника ABC
пересекает прямую BC
в точке X
(см. рис.), касательная в точке B
пересекает прямую AC
в точке Y
, касательная в точке C
пересекает прямую AB
а точке Z
. Докажите, что точки X
, Y
, Z
лежат на одной прямой.
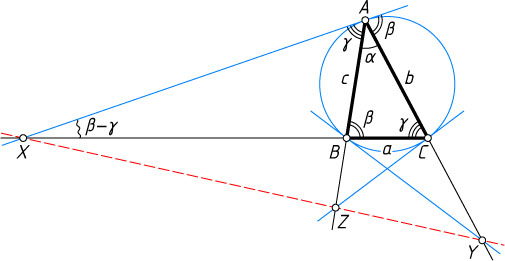
Решение. Пусть BC=a
, AC=b
и AB=c
, а углы при вершинах A
, B
и C
треугольника ABC
равны \alpha
, \beta
и \gamma
соответственно. Тогда по теореме об угле между касательной и хордой
\angle BAX=\angle ACB=\gamma,
а по теореме о внешнем угле треугольника
\angle BXA=\beta-\gamma.
По теореме синусов из треугольника BAX
получаем
\frac{c}{\sin(\beta-\gamma)}=\frac{XB}{\sin\gamma}~\Rightarrow~XB=\frac{c\sin\gamma}{\sin(\beta-\gamma)}.
Аналогично, из треугольника CAX
получаем
XC=\frac{b\sin\beta}{\sin(\beta-\gamma)}.
Значит,
\frac{XB}{XC}=\frac{\frac{c\sin\gamma}{\sin(\beta-\gamma)}}{\frac{b\sin\beta}{\sin(\beta-\gamma)}}=\frac{c\sin\gamma}{b\sin\beta}=\frac{c}{b}\cdot\frac{\sin\gamma}{\sin\beta}=\frac{c}{b}\cdot\frac{c}{b}=\frac{c^{2}}{b^{2}}.
Аналогично,
\frac{YC}{YA}=\frac{a^{2}}{c^{2}},~\frac{ZA}{ZB}=\frac{b^{2}}{a^{2}}.
Тогда
\frac{XB}{XC}\cdot\frac{YC}{YA}\cdot\frac{ZA}{ZB}=\frac{c^{2}}{b^{2}}\cdot\frac{a^{2}}{c^{2}}\cdot\frac{b^{2}}{a^{2}}=1.
Следовательно, по теореме Менелая (см задачу 1622) точки X
, Y
, Z
лежат на одной прямой. Что и требовалось доказать.
Примечание. Если рассматривать треугольник ABC
как вырожденный вписанный шестиугольник, то утверждение задачи следует из теоремы Паскаля (см. задачу 6390).
Источник: Журнал «Crux Mathematicorum». — 1992, № 6, задача 3, с. 170; 1998, № 1, задача 7 (1997, с. 129), с. 3
Источник: Сингапурские математические олимпиады. — 1991
Источник: Posamentier A. S., Salkind Ch. T. Challenging Problems in Geometry. — N.Y.: Dover Publication, 2017. — № 8.17, с. 39

