13547. Окружности S_{1}
и S_{2}
с центрами O_{1}
и O_{2}
соответственно пересекаются в точках A
и B
. Прямая l
, проходящая через точку A
, вторично пересекает эти окружности в точках C
и D
соответственно. Прямые CO_{1}
и DO_{2}
пересекаются в точке P
, а прямая m
, проходящая через точку P
перпендикулярно прямой l
, пересекает прямую AB
в точке Q
. Докажите, что точки P
, D
, Q
, C
и B
лежат на одной окружности.
Решение. Заметим, что конфигурация, соответствующая условию задачи, определена, если прямые AB
и AC
не перпендикулярны.
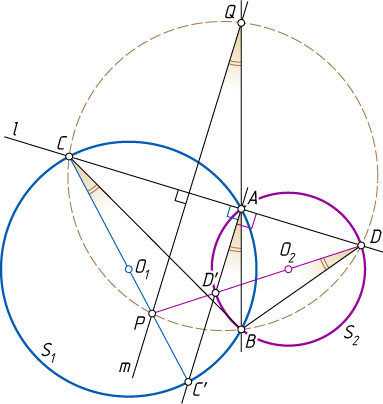
Рассмотрим случай, изображённый на рисунке.
Пусть CC'
и DD'
— диаметры окружностей S_{1}
и S_{2}
соответственно. Тогда
\angle DAD'=\angle CAC'=90^{\circ},
поэтому точки A
, C'
, D'
лежат на одной прямой, так как AC'\perp CD
и PQ\perp CD
, то AC'\parallel PQ
. Тогда
\angle PCB=\angle C'CB=\angle C'AB=\angle PQB,
и точки P
, B
, Q
, C
лежат на одной окружности (см. задачу 12). Кроме того,
\angle D'AB=\angle D'DB=\angle PDB,
поэтому точки P
, B
, Q
и D
тоже лежат на одной окружности. Следовательно, точки P
, D
, Q
, C
и B
лежат на одной окружности. Что и требовалось доказать.
Аналогично для любого другого случая.
Примечание. Разбора случаев можно избежать, если рассматривать ориентированные углы (см. задачу 873).
Источник: Журнал «Crux Mathematicorum». — 1994, № 8, задача 1885 (265), с. 234
