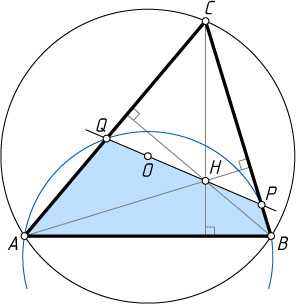
13638. Треугольник ABC
со сторонами BC=a
, AC=b
, AB=c
вписан в окружность радиуса R
с центром O
. Точка H
— ортоцентр треугольника, а прямая OH
пересекает прямые CB
и CA
в точках P
и Q
соответственно (см. рис.).
а) Докажите, что четырёхугольник ABPQ
вписанный тогда и только тогда, когда a^{2}+b^{2}=6R^{2}
.
б) При условии, что четырёхугольник ABPQ
вписанный, выразите PQ
через a
, b
и c
.
Ответ. б) \frac{c(a^{2}+b^{2})}{3ab}=\frac{abc^{3}}{8p(p-a)(p-b)(p-c)}=\frac{2abc^{3}}{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}
.
Решение. Обозначим, углы треугольника, противолежащие сторонам BC
, AC
и AB
через \alpha
, \beta
и \gamma
соответственно.
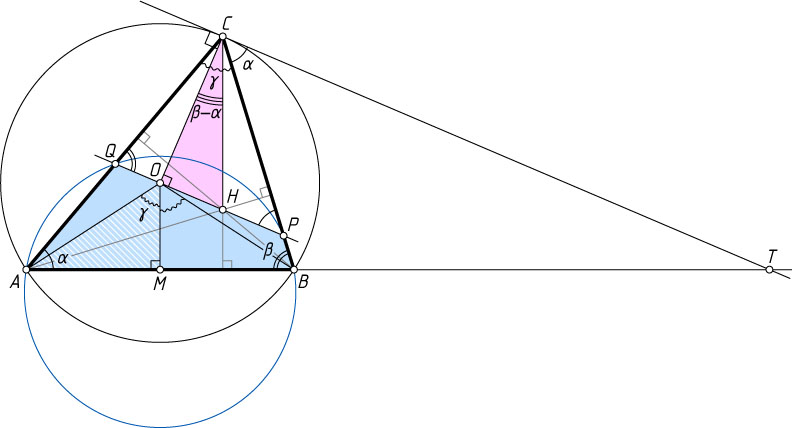
а) 1. Докажем сначала, что четырёхугольник ABPQ
вписанный тогда и только тогда, когда прямая Эйлера треугольника ABC
перпендикулярна радиусу OC
, т. е. OH\perp CO
.
Предположим, что AC\ne BC
и \alpha\lt\beta
. Пусть касательная к описанной окружности треугольника ABC
пересекает прямую AB
точке T
(точка B
между A
и T
). Тогда из теоремы об угле между касательной и хордой следует, что
\angle TCB=\angle BAC=\alpha.
Кроме того, радиус OC
перпендикулярен касательной CT
.
Четырёхугольник ABPQ
вписанный тогда и только тогда, когда
\angle CPQ=\angle CAB=\angle TCB=\alpha,
что равносильно параллельности CT
и OH
, или OH\perp CO
. Утверждение 1 доказано.
2. Пусть M
— середина стороны AB
. Тогда (см. задачу 1257)
CH=2OM=2\cdot AM\ctg\frac{1}{2}\ctg\angle AOB=2\cdot\frac{1}{2}c\ctg\gamma=
=c\ctg\gamma=2R\sin\gamma\cdot\frac{\cos\gamma}{\sin\gamma}=2R\cos\gamma.
Кроме того (см. задачу 20),
\angle OCH=|\angle ACB-\angle ACO-\angle BCH|=|\gamma-(90^{\circ}-\beta)-(90^{\circ}-\beta)|=
=|\gamma-180^{\circ}+2\beta|=|180^{\circ}-\gamma-2\beta|=|\alpha+\beta-2\beta|=|\alpha-\beta|=\beta-\alpha.
3. Заметим, что
CO\perp=OH~\Leftrightarrow~CH\cos\angle OCH~\Leftrightarrow~R=2R\cos\gamma\cos(\beta-\gamma)~\Leftrightarrow
\Leftrightarrow~1=-2\cos(\alpha+\beta)\cos(\alpha-\beta)~\Leftrightarrow~-1=\cos2\alpha+\cos2\beta~\Leftrightarrow
\Leftrightarrow~-1=1-2\sin^{2}\alpha+1-2\sin^{2}\beta~\Leftrightarrow~2\sin^{2}\alpha+2\sin^{2}\beta=3~\Leftrightarrow
\Leftrightarrow~4R^{2}\sin^{2}\alpha+4R^{2}\sin^{2}\beta=6R^{2}~\Leftrightarrow~a^{2}+b^{2}=6R^{2}.
Отсюда следует утверждение пункта а).
б) Треугольники CPQ
и CAB
подобны по двум углам, поэтому
\frac{PQ}{AB}=\frac{CP}{CA}~\Rightarrow~PQ=\frac{AB}{CA}\cdot CP=\frac{c}{b}CP.
С другой стороны, поскольку CO\perp PO
и \angle OPC=\alpha
, то
CO=CP\sin\alpha=CP\cdot\frac{a}{2R}~\Rightarrow~CP=CO\cdot{2R}{a}=\frac{2R^{2}}{a}.
Следовательно,
PQ=\frac{c}{b}CP=\frac{c}{b}\cdot\frac{2R^{2}}{a}=\frac{2cR^{2}}{ab}=\frac{2c(a^{2}+b^{2})}{6ab}=\frac{c(a^{2}+b^{2})}{3ab}.
Если применить формулы S=\frac{abc}{4R}
, и S=\sqrt{p(p-a)(p-b)(p-c)}
, где S
— площадь, то можно получить ответ в виде
PQ=\frac{abc^{3}}{8p(p-a)(p-b)(p-c)}=\frac{2abc^{3}}{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}.
Источник: Журнал «Crux Mathematicorum». — 2000, № 1, задача 2409 (1999, с. 49), с. 57; 2011, № 4, задача 3541 (2010, с. 240, 242), с. 243

