13708. Окружность \Gamma
с диаметром AB
и окружность \Omega
с центром A
пересекаются в точках C
и D
. Точка M
, отличная от C
и D
, лежит на окружности \Omega
. Прямые BM
, CM
и DM
вторично пересекают окружность \Gamma
в точках N
, P
и Q
соответственно. Докажите, что:
а) четырёхугольник MPBQ
— параллелограмм;
б) отрезок MN
— среднее геометрическое отрезков NC
и ND
.
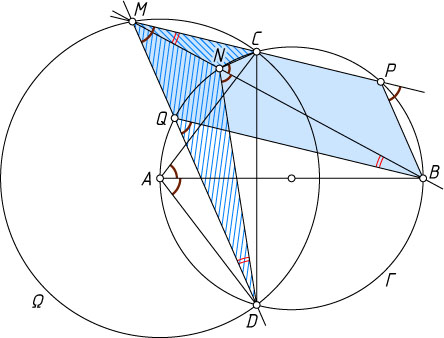
Решение. Рассмотрим случай, изображённый на рисунке. Для любого другого случая решение аналогично.
а) Прямая AB
— серединный перпендикуляр к отрезку CD
(см. задачу 1130), поэтому \angle CAB=\angle BAD
, а так как
\angle CMQ=\frac{1}{2}\angle CAD=\angle BAD=\angle BQD=180^{\circ}-\angle BQM,
то CM\parallel QB
, т. е. MP\parallel BQ
.
Поскольку
\angle CPB=180^{\circ}-\angle CAB=180^{\circ}-\frac{1}{2}\angle CAD=180^{\circ}-\angle CMQ,
то PB\parallel MQ
. Следовательно, MPBQ
— параллелограмм.
б) Из параллельности CM
и BQ
получаем
\angle CMN=\angle QBN=\angle QDN=\angle MDN,
а так как
\angle CNM=180^{\circ}-\angle BNC=180^{\circ}-\angle BAC=
=180^{\circ}-\angle BAD=180^{\circ}-\angle BND=\angle MND,
то треугольники NMC
и NDM
подобны по двум углам. Значит, \frac{NM}{ND}=\frac{NC}{NM}
. Следовательно, MN^{2}=NC\cdot ND
. Что и требовалось доказать.
Примечание. См. также решение задачи 124.