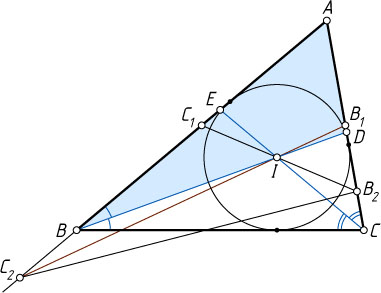
13770. Точки B_{1}
и C_{1}
— середины сторон соответственно AC
и AB
треугольника ABC
, I
— центр вписанной окружности треугольника. Прямые B_{1}I
и C_{1}I
пересекают прямые AB
и AC
в точках C_{2}
и B_{2}
соответственно. Найдите угол BAC
, если треугольники ABC
и AB_{2}C_{2}
равновелики.
Ответ. 60^{\circ}
.
Решение. Обозначим BC=a
, CA=b
, AB=c
, AC_{2}=x
, AB_{2}=y
. Треугольники ABC
и AB_{2}C_{2}
равновелики, поэтому xy=bc
.
Пусть BD
и CE
— биссектрисы треугольника ABC
. Тогда (см. задачу 1509 и 2906)
AD=\frac{bc}{a+c},~AE=\frac{bc}{a+b},~\frac{BI}{ID}=\frac{a+c}{b},~\frac{CI}{IE}=\frac{a+b}{c}.
Случай 1. Пусть c=a
. Тогда точка B_{1}
совпадает с D
. Тогда треугольник ABC
равнобедренный, AB=BC
, поэтому точка C_{2}
совпадает с B
, x=c
, а так как xy=bc
, то y=b
. Значит, точка B_{2}
совпадает с C
, поэтому AC=BC
. Следовательно, треугольник ABC
равносторонний, и \angle BAC=60^{\circ}
.
Случай 2. c\gt a
.
Тогда CD\lt AD
, а так как AB_{1}=\frac{1}{2}AC
, то точка D
лежит между C
и B_{1}
. Значит, точка C_{2}
пересечения прямых B_{1}I
и AB
лежит на продолжении стороны AB
за точку B
. Следовательно,
x=AC_{2}\gt AB\gt c~\Rightarrow~y=\frac{bc}{x}\lt b.
По теореме Менелая для треугольника ABD
и прямой B_{1}C_{2}
получаем
\frac{AC_{2}}{C_{2}B}\cdot\frac{BI}{ID}\cdot\frac{DB_{1}}{B_{1}A}=1,
а так как
DB_{1}=AD-AB_{1}=\frac{bc}{a+c}-\frac{b}{2}=\frac{b(c-a)}{2(a+c)},
то \frac{DB_{1}}{B_{1}A}=\frac{c-a}{a+c}
. Значит,
\frac{x}{x-c}\cdot\frac{a+c}{b}\cdot\frac{c-a}{a+c}=1,~\mbox{или}~\frac{x}{x-c}=\frac{b}{c-a},
откуда x=\frac{bc}{b-c+a}
.
Аналогично находим, что y=\frac{bc}{c-b+a}
, а так как xy=bc
, то
\frac{b^{2}c^{2}}{(b-c+a)(c-b+a)}=bc~\Rightarrow~a^{2}-(b-c)^{2}=bc~\Rightarrow
\Rightarrow~a^{2}=b^{2}+c^{2}-bc=b^{2}+c^{2}-2bc\cdot\frac{1}{2}=b^{2}+c^{2}-2bc\cos\angle BAC~\Rightarrow
\Rightarrow~\cos\angle BAC=\frac{1}{2}~\Rightarrow~\angle BAC=60^{\circ}.
Что и требовалось доказать.
Аналогично для случая c\lt a
.
Источник: Журнал «Crux Mathematicorum». — 2005, № 8, задача 5, с. 512
Источник: Венгерско-израильская математическая олимпиада. — 2001
