13829. Биссектрисы внутреннего и внешнего углов при вершине A
треугольника ABC
пересекают описанную окружность этого треугольника в точках D
и E
соответственно. Точка F
симметрична A
относительно точки D
, а точка G
симметрична A
относительно точки E
. Описанные окружности треугольников ADG
и AEF
пересекаются в точке P
, отличной от A
. Докажите, что AP\parallel BC
.
Решение. Биссектрисы смежных углов перпендикулярны, т. е. \angle DAE=90^{\circ}
, поэтому DE
— диаметр описанной окружности \Gamma
треугольника ABC
.
Пусть O_{1}
и O_{2}
— центры описанных окружностей треугольников ADG
и AEF
соответственно. Линия центров пересекающихся окружностей перпендикулярна из общей хорде (см. задачу 1130), поэтому O_{1}O_{2}\perp AP
.
Достроим треугольник ADE
до прямоугольника ADTE
. Точка O_{1}
— середина гипотенузы DG
прямоугольного треугольника ADG
, а так как DT=AE=EG
и DT\parallel EG
, то DEGT
— параллелограмм. Значит, середина O_{1}
его диагонали DG
является серединой диагонали ET
. Аналогично, точка O_{2}
— середина отрезка DT
. Следовательно, по теореме о средней линии треугольника O_{1}O_{2}\parallel DE
.
Точка D
окружности \Gamma
— середина дуги BC
, не содержащей точки A
(см. задачу 430), а DE
— диаметр этой окружности, поэтому DE\perp BC
. Тогда O_{1}O_{2}\perp BC
. Значит, прямая AP
, перпендикулярная O_{1}O_{2}
, также перпендикулярна DE
, а следовательно, AP\parallel BC
. Что и требовалось доказать.
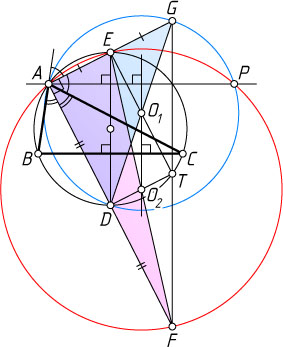
Источник: Журнал «Crux Mathematicorum». — 2008, № 6, задача 3, с. 348
Источник: Тайваньские математические олимпиады. — 2004
