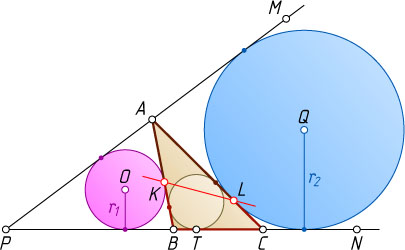
13926. Сторона BC
треугольника ABC
лежит на отрезке PN
, а вершина A
— на отрезке PM
(см. рис.). Окружность с центром O
и радиусом r_{1}
— вписанная окружность треугольника APB
, а окружность с центром Q
и радиусом r_{2}
— вневписанная окружность треугольника APC
, касающаяся стороны AC
, причём первая окружность касается стороны AB
в точке K
, вторая окружность касается стороны AC
в точке L
, а вписанная окружность треугольника ABC
касается стороны BC
в точке T
. Докажите, что:
а) прямая KL
делит периметр треугольника ABC
пополам;
б) площадь треугольника ABC
равна TC\cdot r_{1}+TB\cdot r_{2}
.
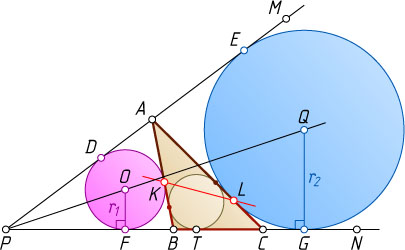
Решение. Пусть окружности с центрами O
и Q
касаются прямой PM
в точках D
и E
соответственно, а прямой PN
— в точках F
и G
соответственно.
а) Поскольку
DE=PE-PD=PG-PF=FG,
то
AK+AL=AD+AE=DE=FG=
=BF+BC+CG=BK+BC+CL.
Отсюда следует утверждение пункта а).
б) Пусть p
— полупериметр треугольника ABC
. Тогда
AB+TC=AK+KB+TC=p~\mbox{и}~AC+TB=AL+LC+TB=p,
а также согласно предыдущему пункту
p=AK+AL=AD+AE=DE=FG,
так что удвоенная площадь прямоугольной трапеции OFGQ
равна
2S_{OFGQ}=2\cdot FG\cdot\frac{OF+QG}{2}=p(r_{1}+r_{2})=(AB+TC)r_{1}+(AC+TB)r_{2}.
С другой стороны,
2S_{OFGQ}=2S_{\triangle PGQ}-2S_{\triangle PFO}=PG\cdot r_{2}-PF\cdot r_{1}.
Таким образом,
(AB+TC)r_{1}+(AC+TB)r_{2}=PG\cdot r_{2}-PF\cdot r_{1},
или
TC\cdot r_{1}+TB\cdot r_{2}=(PG-AC)r_{2}-(PF+AB)r_{1},
а так как окружность радиуса r_{2}
является вневписанной для треугольника PAC
, а окружность радиуса r_{1}
является вписанной для треугольника APB
, то (см. задачи 392 и 452)
(PG-AC)r_{2}=(p_{\triangle PAC}-AC)r_{2}=S_{\triangle PAC}~\mbox{и}~(PF+AB)r_{1}=p_{\triangle PAB}r_{1}=S_{\triangle PAB}.
Следовательно,
TC\cdot r_{1}+TB\cdot r_{2}=S_{\triangle PAC}-S_{\triangle PAB}=S_{\triangle ABC}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2013, № 3, задача CC13, с. 119

