13932. Окружности с центрами O_{1}
и O_{2}
, построенные как на диаметрах на хордах соответственно AB
и CD
окружности \Gamma
, касаются внешним образом. Прямая O_{1}O_{2}
пересекает окружность \Gamma
в точках E
и F
. Известно, что O_{1}A=a
, O_{2}C=b
, O_{1}E=x
и O_{2}F=y
. Докажите, что a-b=x-y
.
Решение. Пусть окружности с диаметрами AB
и CD
касаются в точке T
. Тогда точки E
, O_{1}
, T
, O_{2}
и F
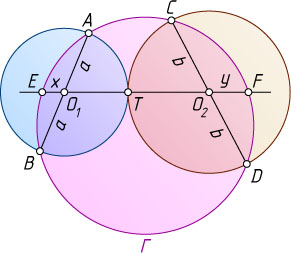
лежат на одной прямой (см. задачу 1758). Без ограничения общности будем считать, что они расположены в указанном порядке (см. рис.). Тогда
O_{1}F=O_{1}T+TO_{2}+O_{2}F=a+b+y.
Аналогично,
O_{2}E=b+a+x.
По теореме о произведениях пересекающихся хорд (см. задачу 2627)
AO_{1}\cdot O_{1}B=EO_{1}\cdot O_{1}F,~\mbox{или}~a^{2}=x(a+b+y).
Аналогично, b^{2}=y(a+b+x)
. Тогда
(a+b)(a-b)=a^{2}-b^{2}=x(a+b+y)-y(a+b+x)=
=x(a+b)-y(a+b)=(a+b)(x-y).
Следовательно,
a-b=x-y.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2013, № 6, задача 3753 (2012, с. 241, 243), с. 279
