1402. Угол треугольника равен 60^{\circ}
. Докажите, что центр вписанной окружности равноудалён от центра описанной окружности и точки пересечения высот.
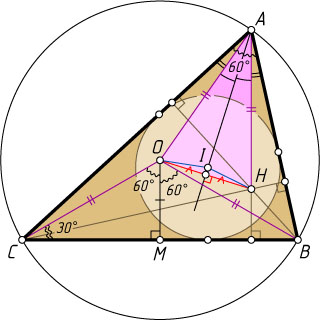
Решение. Пусть H
— точка пересечения высот треугольника ABC
, \angle BAC=60^{\circ}
, I
— центр вписанной окружности, O
— центр описанной окружности, M
— середина стороны BC
.
Известно, что в любом треугольнике \angle OAC=\angle HAB
(см. задачу 20), поэтому биссектриса AI
угла BAC
является также биссектрисой угла OAH
. Известно также, что AH=2OM
(см. задачу 1257).
Предположим, что треугольник ABC
остроугольный. Поскольку MOC
— половина центрального угла BOC
, равного 120^{\circ}
, то \angle OCM=30^{\circ}
, поэтому AO=OC=2OM=AH
. Значит, треугольник OAH
равнобедренный, его биссектриса, проведённая из вершины A
, лежит на серединном перпендикуляре к основанию OH
. Точка I
лежит на этой биссектрисе, следовательно, она равноудалена от точек O
и H
.
Аналогично для тупоугольного треугольника.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4.20, с. 43
