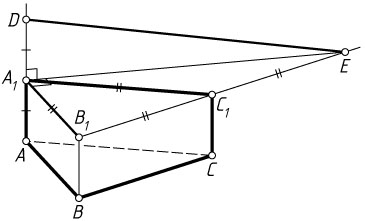
14088. В основании правильной треугольной призмы ABCA_{1}B_{1}C_{1}
лежит треугольник ABC
. На прямой AA_{1}
отмечена такая точка D
, что точка A_{1}
— середина отрезка AD
. На прямой B_{1}C_{1}
отмечена точка E
так, что C_{1}
— середина отрезка B_{1}E
.
а) Докажите, что прямые A_{1}B_{1}
и DE
перпендикулярны.
б) Найдите расстояние между прямыми AB
и DE
, если AB=3
, AA_{1}=1
.
Ответ. \frac{3\sqrt{21}}{7}
.
Решение. а) В треугольнике A_{1}B_{1}E
медиана A_{1}C_{1}
равна половине стороны B_{1}E
, значит, этот треугольник прямоугольный, \angle B_{1}A_{1}E=90^{\circ}
. Ортогональная проекция A_{1}E
наклонной DE
на плоскость A_{1}B_{1}C_{1}
перпендикулярна прямой A_{1}B_{1}
, лежащей в этой плоскости. Следовательно, по теореме о трёх перпендикулярах DE\perp A_{1}B_{1}
. Что и требовалось доказать.
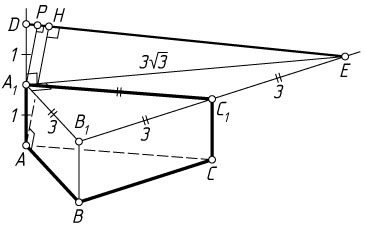
б) Опустим перпендикуляр AH
на прямую DE
. Прямая AB
, параллельная A_{1}B_{1}
, перпендикулярна пересекающимся прямым AD
и A_{1}E
плоскости DEA_{1}
, значит, прямая AB
перпендикулярна этой плоскости, поэтому AB\perp AH
. Следовательно, AH
— общий перпендикуляр скрещивающихся прямых AB
и DE
, а расстояние между этими прямыми равно длине отрезка AH
.
Из прямоугольного треугольника A_{1}B_{1}E
находим, что
A_{1}E=A_{1}B_{1}\tg60^{\circ}=3\sqrt{3}.
Пусть A_{1}P
— высота прямоугольного треугольника DEA_{1}
, проведённая из вершины прямого угла. Тогда A_{1}P
— средняя линия треугольника ADH
. Следовательно (см. задачи 1880 и 1967),
AH=2A_{1}P=2\cdot\frac{A_{1}D\cdot A_{1}E}{DE}=2\cdot\frac{A_{1}D\cdot A_{1}E}{\sqrt{A_{1}D^{2}+A_{1}E^{2}}}=
=2\cdot\frac{1\cdot3\sqrt{3}}{\sqrt{1+27}}=\frac{2\cdot3\sqrt{3}}{\sqrt{28}}=\frac{3\sqrt{3}}{\sqrt{7}}=\frac{3\sqrt{21}}{7}.
Источник: ЕГЭ. — 2021, 29 июня, задача 14

