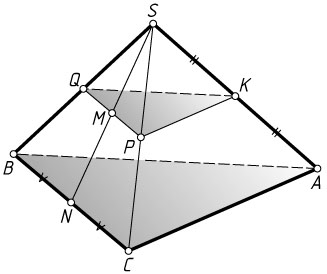
14090. Дана правильная треугольная пирамида SABC
, AB=24
, высота SH
, проведённая к основанию, равна 14, точка K
— середина AS
, точка N
— середина BC
. Плоскость, проходящая через точку K
и параллельная основанию пирамиды, пересекает рёбра SB
и SC
в точках Q
и P
соответственно.
а) Докажите, что PQ
проходит через середину отрезка SN
.
б) Найдите угол между плоскостью основания и плоскостью APQ
.
Ответ. \arctg\frac{7\sqrt{3}}{30}
.
Решение. а) Если две параллельные плоскости пересечь третьей, то в пересечениях образуются параллельные прямые (см. задачу 8009), значит, KQ\parallel AB
и KP\parallel AC
, а так как K
— середина ребра SA
, то по теореме Фалеса Q
и P
— середины рёбер SB
и SC
соответственно, а PQ
— средняя линия треугольника BSC
. Медиана SN
и средняя линия PQ
этого треугольника делят друг друга пополам (см. задачу 1881), следовательно, отрезок PQ
проходит через середину M
отрезка SN
. Что и требовалось доказать.
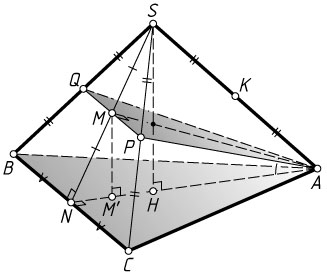
б) Опустим перпендикуляр MM'
на прямую AN
. Тогда MM'
— перпендикуляр к плоскости ABC
, а линейный угол двугранного угла, образованного плоскостями APQ
и ABC
, — это угол MAM'
. В прямоугольном треугольнике AMM'
известны катеты
MM'=\frac{1}{2}SH=7,~AM'=AH+\frac{1}{2}HN=AH+\frac{1}{4}AH=\frac{5}{4}\cdot\frac{24\sqrt{3}}{3}=10\sqrt{3}.
Следовательно,
\tg\angle MAM'=\frac{MM'}{AM'}=\frac{7}{10\sqrt{3}}=\frac{7\sqrt{3}}{30}.
Источник: ЕГЭ. — 2021, задача 14

