1491. Найдите периметр треугольника ABC
, если BC=a
и отрезок прямой, касательной ко вписанному кругу и параллельной BC
, заключённый внутри треугольника, равен b
.
Ответ. \frac{2a^{2}}{a-b}
.
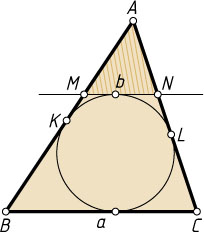
Решение. Пусть указанная касательная пересекает стороны AB
и BC
треугольника ABC
в точках M
и N
соответственно, а вписанная окружность треугольника касается этих сторон в точках соответственно K
и L
. Обозначим через p
полупериметр треугольника ABC
. Тогда AL=AK=p-BC=p-a
(см. задачу 219). С другой стороны, полупериметр треугольника AMN
также равен отрезку AK
(см. задачу 4805), а так как треугольник AMN
подобен треугольнику ABC
, то \frac{p-a}{p}=\frac{b}{a}
. Отсюда находим, что p=\frac{a^{2}}{a-b}
. Следовательно, периметр треугольника ABC
равен \frac{2a^{2}}{a-b}
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 263, с. 30
