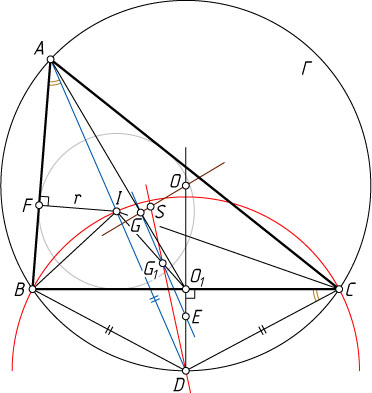
16028. Точка I
— центр вписанной окружности треугольника ABC
. Докажите, что прямые Эйлера треугольников IBC
, ICA
, IAB
и ABC
пересекаются в одной точке.
Решение. Пусть r
— радиус вписанной окружности треугольника ABC
, O
и R
— соответственно центр и радиус описанной окружности \Gamma
треугольника, G
— точка пересечения медиан. Тогда GO
— прямая Эйлера треугольника ABC
.
Пусть D
— пересечения луча AI
с окружностью \Gamma
. Тогда D
— середина дуги BC
, а из теоремы о трилистнике (см. задачу 788) следует, что D
— центр описанной окружности треугольник IBC
.
Пусть G_{1}
— точка пересечения медиан треугольника IBC
. Тогда DG_{1}
— прямая Эйлера этого треугольника.
Пусть O_{1}
— середина стороны BC
. Поскольку G
и G_{1}
— точки пересечения медиан треугольников, то
\frac{AG}{GO_{1}}=\frac{IG_{1}}{G_{1}O_{1}}=2~\Rightarrow~GG_{1}\parallel AD.
Тогда, если E
— точка пересечения GG_{1}
и OD
, то по теореме о пропорциональных отрезках отрезках на параллельных прямых (см. задачу 1597)
\frac{GG_{1}}{G_{1}E}=\frac{AI}{ID}~\mbox{и}~DE=\frac{2}{3}DO_{1}.
Прямая Эйлера DG_{1}
треугольника IBC
пересекает прямую Эйлера GO
треугольника ABC
в некоторой точке S
, лежащей между G
и O
(см. задачу 806).
Пусть IF
— перпендикуляр к AB
. Поскольку \angle BAD=\angle BCD
как вписанные углы, опирающиеся на одну и ту же дугу, то прямоугольные треугольники AFI
и CO_{1}D
подобны, поэтому
\frac{IA}{CD}=\frac{FI}{O_{1}D}=\frac{r}{O_{1}D}.
По теореме Менелая для треугольника GOE
и прямой DS
получаем
1=\frac{GS}{SO}\cdot\frac{OD}{DE}\cdot\frac{EG_{1}}{G_{1}G}=\frac{GS}{SO}\cdot\frac{OD}{DE}\cdot\frac{ID}{AI}=\frac{GS}{SO}\cdot\frac{OD}{DE}\cdot\frac{CD}{AI}=
=\frac{GS}{SO}\cdot\frac{R}{\frac{2}{3}DO_{1}}\cdot\frac{DO_{1}}{r}=\frac{GS}{SO}\cdot\frac{3R}{2}\cdot\frac{1}{r}=\frac{GS}{SO}\cdot\frac{3R}{2r},
откуда \frac{GS}{SO}=\frac{2r}{3R}
.
Из аналогичных рассуждений для треугольников IAB
и ICA
получим то же самое отношение. Следовательно, их прямые Эйлера проходят через ту же самую точку S
(точка Шиффлера треугольника ABC
).
Источник: Журнал «Crux Mathematicorum». — 1986, № 6, задача 1018 (1985, с. 51), с. 150
